在使用梯度下降法进行回归时,需要频繁的进行偏导数的计算。在很多的相关介绍中会展示使用计算图进行偏导数的计算。这里简述对该方法的一些理解。
概述
- 计算图求导,可以理解为是对求导的链式法则的图表示
- 在计算图中,在一个单向路径上的算子,求导时,将各个导数相乘即可
- 在计算图中,在一个单向路径上,上一个节点的输出,是下一个节点的输入;函数关系上,就是 \( f(g(x)) \),即\( g(x) \)的输出是,\( f(x) \)的输入
- 一个节点的两个入度(分支),求导时,将各个导数相乘即可
- 多元函数求偏导时,只需要关注其偏导的变量即可
链式法则的典型形式
这里对求导的链式法则的典型形式做一个简单的回顾。
在对复杂的表达式求导/微分时,有时候看起来会很复杂。如果能够灵活的使用链式法则可以巧妙将复杂函数的求导转换为简单函数的求导。
法则1:
$$
f(x) = g(h(x))
\\
f'(x) = \frac{\partial f}{\partial x} = \frac{\partial g}{\partial h} \frac{\partial h}{\partial x}
$$
例如,使用该法则可以很简单对如下函数求导:
$$
f(x) = e^{(x^2)}
\\
g(h) = e^h \, h(x) = x^2
\\
f'(x) = \frac{\partial g}{\partial h} \frac{\partial h}{\partial x} = e^h * 2 * x = 2x*e^h = 2xe^{x^2}
$$
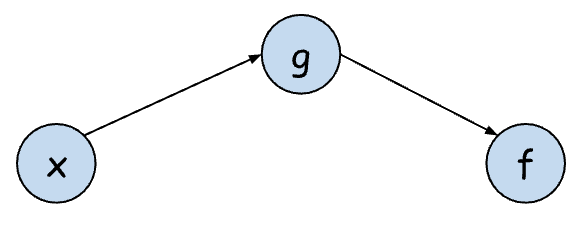
如果使用计算图的方式表达如上的求导,如下:
$$
f(x) = f(g(x))
\\
\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g}\frac{\partial g}{\partial h}
$$
所以:在计算图中,在一个单向路径上的算子,求导时,将各个导数相乘即可。
法则2:
$$
f(x) = f(u(x),(v(x))
\\
f'(x) = \frac{\partial f}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial f}{\partial v} \frac{\partial v}{\partial x}
$$
可以使用上面公式,做如下的求导:
$$
f(x) = x*e^x
\\
u(x) = x \, , v(x) = e^x ,\, f(u,v) = u*v
\\
f'(x) = \frac{\partial f}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial f}{\partial v} \frac{\partial v}{\partial x} = v*1 + u*e^x = e^x + x*e^x
$$
(注:当然上面的函数求导最好用乘法法则去求导,完全没有必要使用上面的方法,这里只是演示该方法的使用)
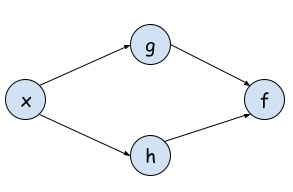
使用计算图表示该求导:
$$
f(x) = f(g,h) g=g(x) h=h(x)
\\
\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g}\frac{\partial g}{\partial x} + \frac{\partial f}{\partial h}\frac{\partial h}{\partial x}
$$
所以:一个节点的两个入度(分支),求导时,将各个路径上的导数相加即可。
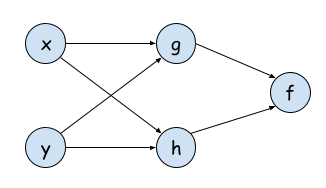
多元函数的场景:
$$
f = f(x,y) = f(g,h) = f(g(x,y),g(x,y))
\\
\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g}\frac{\partial g}{\partial x} + \frac{\partial f}{\partial h}\frac{\partial h}{\partial x}
\\
\frac{\partial f}{\partial y} = \frac{\partial f}{\partial g}\frac{\partial g}{\partial y} + \frac{\partial f}{\partial h}\frac{\partial h}{\partial y}
$$
对于多元函数场景,因为我们总是关注的时是一个分量的偏导数,所以其计算法则如上。神经网络中的相关计算,与上述计算非常类似,这里不再详述。
附录:对乘法求导
$$
f(x) = g(x)h(x)
\\
f'(x) = g(x)h'(x) + g'(x)h(x)
$$
结合简单函数求导、乘法法则、链式法则,可以对更复杂的函数进行求导:
$$
f(x) = xe^{x^2}
\\
u(x) = x \, g(x) = e^{(x^2)}
\\
g'(x) = \frac{\partial g}{\partial h} \frac{\partial h}{\partial x} = 2xe^{x^2}
\\
f'(x) = u'(x)g(x) + u(x)g'(x) = g(x) + u(x)g'(x) = e^{x^2} + x*2xe^{x^2} = e^{x^2} + 2x^2e^{x^2}
$$
Leave a Reply