在2015年,由 OpenAI 的 DP Kingma 等发布了 《ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION》算法后,由于其迭代效率提升非常明显,所以 ADAM(或其变种)就被广泛的采用。本文将继续对上一篇介绍的梯度下降算法进行优化,并介绍 ADAM 算法(一种对随机梯度下降算法的优化算法)的实现以及效果。
Stochastic Gradient Descent 或者说 mini-batch解决了样本量巨大时,梯度下降迭代的问题。但是,也带了一些新的问题。最为主要的是,因为样本数据的波动,而导致每次梯度下降计算时,梯度方向的波动,从而降低了梯度下降迭代的效率。
在前面的《Mini-batch Gradient Descent和随机梯度下降(SGD)》文章中,我们对比了 mini-batch 和 batch gradient descent 的在迭代时,目标函数下降的速度。
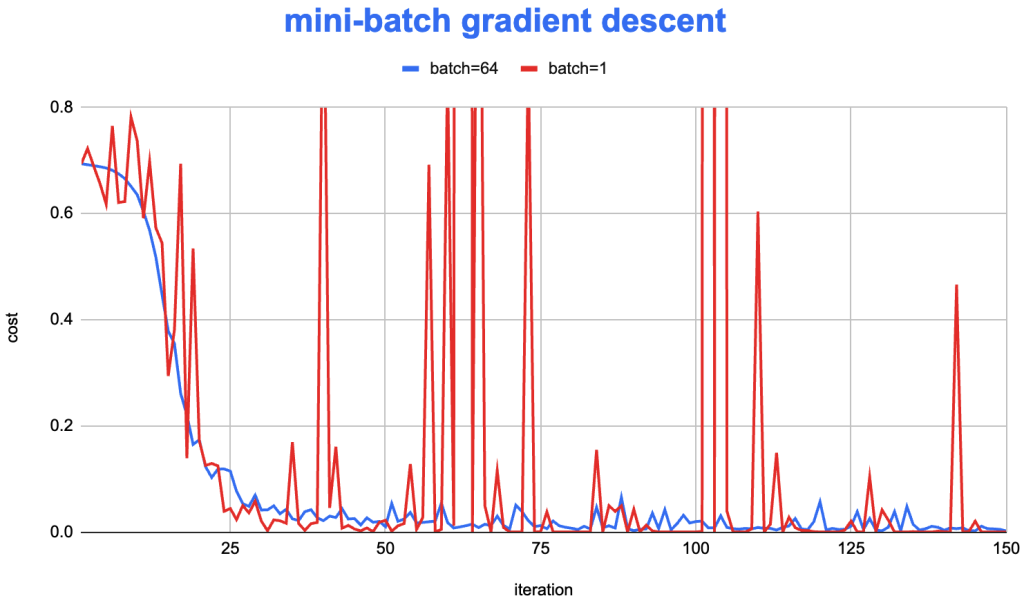
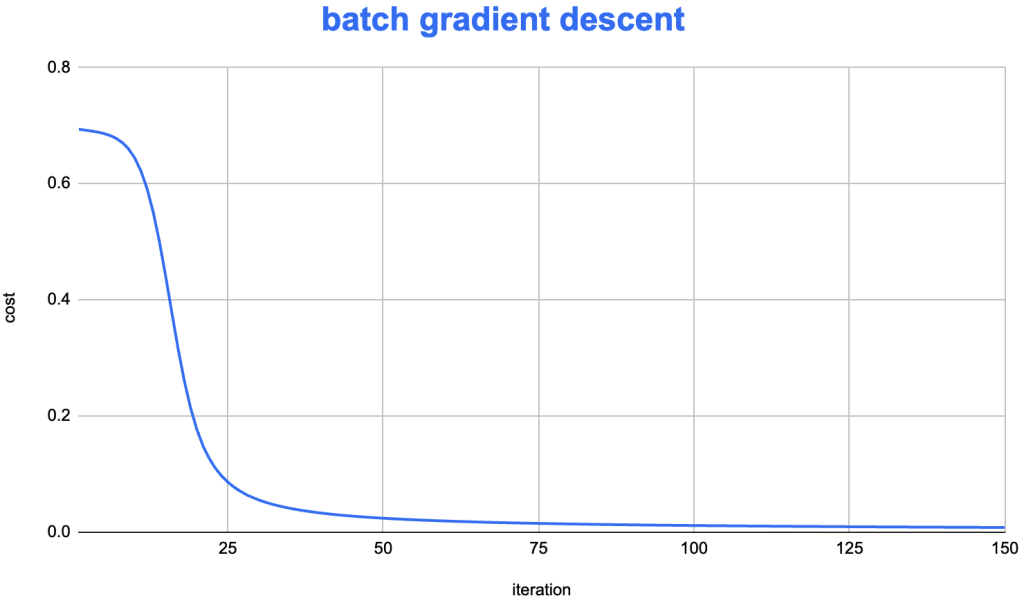
可以看到,batch gradient descent 的目标函数下降非常稳定,而 Mini-batch 的实现则会有明显的波动。为了尝试修正这个问题,从而提高迭代效率,在神经网络算法上,逐渐探索出了一些较为高效的优化算法:Adam SGD。该算法将 RMSprop 和 “Exponential smoothing”的想法结合在一起,形成了一个较为高效的算法,在实践中被广为使用。
目录
Stochastic Gradient Descent 与 Momentum
SGD 会在每次迭代时根据样本的偏差,展现出不同的偏差,所以,在使用SGD进行迭代时,观察其 cost函数下降,应该会有更加明显的波动(后续吧自己实现的程序改造后,尝试观察一下)。
为了加快迭代的速度,一个折中的思路是,引入一个均值替换当前的梯度方向。该如何引入这个均值呢?梯度是一个随时计算推进,不断推进的变量,常用的均值计算可以参考:Moving average。最为常见的实现是使用“Exponential moving average”,这种平均值的计算,在迭代计算时实现非常简单。
Momentum 就是 “Exponential moving average”实现时的参数“smoothing factor”,在神经网络中,经常使用 \( \beta \)表示(原因是 \( \alpha \) 已经表示学习率了 )。
而这里的 Momentum ,也是 TensorFlow 在构造 SGD 算法时需要的另一个参数。
关于Exponential moving average
或者叫“Exponential smoothing”。我们看看这个算法的具体实现是怎样的?
原始的迭代:\( w = w – \alpha \frac{\partial J}{\partial w} \)
使用 “Exponential smoothing” 后的迭代:
$$
\begin{align}
v_0 & = 0 \quad \partial{w}_t = \frac{\partial J}{\partial w}|_{(for \, sample \, t)} \\
v_{t} & = \beta*v_{t-1} + (1-\beta)\partial{w}_{t} \\
w & := w – \alpha v_t
\end{align}
$$
考虑 \( \beta = 0.9 \),如果数学直觉比较好的话,可以看出,原本使用梯度\( \partial{w} \)进行迭代的,这里使用了一个梯度的“Exponential smoothing” \( v_t \)去替代。上面的式子中,\( v_t \) 如果展开有如下表达式:
$$
\begin{align}
v_t & = (1-\beta)\partial{w}_{t} + \beta(1-\beta)\partial{w}_{t-1} + \beta^2(1-\beta)\partial{w}_{t-2} … \\
& = \sum\limits_{i=0}^{t} \beta^{i}(1-\beta)\partial{w}_{i}
\end{align}
$$
使用“Exponential smoothing” 之后,新的迭代方向 \( v_t \),可以理解为一个前面所有梯度方向的加权平均。离得越近的梯度,权重越高,例如,\( \partial{w}_{t} \)的权重是\( (1-\beta) \);而之前的梯度,则每次乘以一个 \( \beta \)衰减。
Exponential moving average的“冷启动问题”与修正
仔细观测上诉的 “Exponential moving average” 公式,可以注意到一个问题,就是其最初的几个点总是会偏小。其原因是,当前值的权重总是为 \( 1- \beta \),而因为是初始的几个值,并没有更前面的数据去“平均”当前值,也就会出现,初始值总是会偏小的问题。
通常,如果样本量很大的事时候,则可以忽略这个问题,因为初始值偏小的点占比会非常少,可以忽略。如果要一定程度上解决这个问题,也有继续对上述的 “Exponential moving average”做了一些修正,可以考虑对 \( v_t \)的结果值做一个修正:\( v_t := \frac{vt}{1-\beta^t} \)。
一般的,因为样本的数量总是比较大的,所以我们可以忽略这个问题,而无需做任何修正。
RMSprop
在前面的“Gradient Descent with Momentum”中,我们看到为了解决梯度波动较大的问题,使用了 “Exponential moving average” 去尝试将一些比较偏的梯度,拉倒一个较为平均的方向上来。RMSprop的想法也是类似的,这里通过了root mean square的想法进行平均值的计算。具体的,在进行 SGD 时,每次更新梯度,按照如下的方法进行更新:
$$
\begin{align}
s_0 & = 0 \quad \partial{w}_t = \frac{\partial J}{\partial w}|_{(for \, sample \, t)} \\
s_{t} & = \beta*s_{t-1} + (1-\beta)(\partial{w}_{t})^2 \\
w & := w – \alpha \frac{\partial w}{\sqrt{s_{t}}}
\end{align}
$$
说明:这里对梯度进行平方时,如果在程序中是一个梯度向量,那么这里“平方”也就是对梯度的每一个分量进行一次平方。
在“Exponential smoothing”的实现中,是将当前值,使用一个加权平均替代。与“Exponential smoothing”类似的,原本的梯度方向,现在使用如下的方向去替代了:
$$
\begin{align}
s_t & = \frac{\partial{w}_{t}}{\sqrt{(1-\beta)(\partial{w}_{t})^2 + \beta(1-\beta)(\partial{w}_{t-1})^2 + \beta^2(1-\beta)(\partial{w}_{t-2})^2 + \cdots }} \\
& = \frac{\partial{w}_{t}}{\sqrt{\sum\limits_{i=1}^{t}\beta^i(1-\beta)(\partial{w}_{i})^2}} \\
\end{align}
$$
Adam Gradient Descent
这可能是实际使用最多的算法,全称是 Adaptive Moment Estimation 。该实现,将 “Momentum” 和 “RMSprop” 做了一定的融合,形成了新的“最佳实践” Adam。在融合上,具体的实现与两个细节点:
(1) 在 Adam 中均使用了“修正”计算,即 \( \hat{v_t} = \frac{v_t}{1-(\beta_1)^t} \quad \hat{s_t} = \frac{s_t}{1-(\beta_1)^t} \)
(2) 参数更新公式,使用了两个算法的融合: \( w := w – \alpha \frac{\hat{v_t}}{\sqrt{\hat{s_t}}} \)
Adam optimization的效果对比
在 Adam 的论文中对于效果做了非常多的评估,感兴趣的可以参考相关论文。
这里根据之前完成的训练程序,也进行了优化,实现了Adam算法。在 MNIST 数据集的训练上,我们来看看 Adam 的效果:
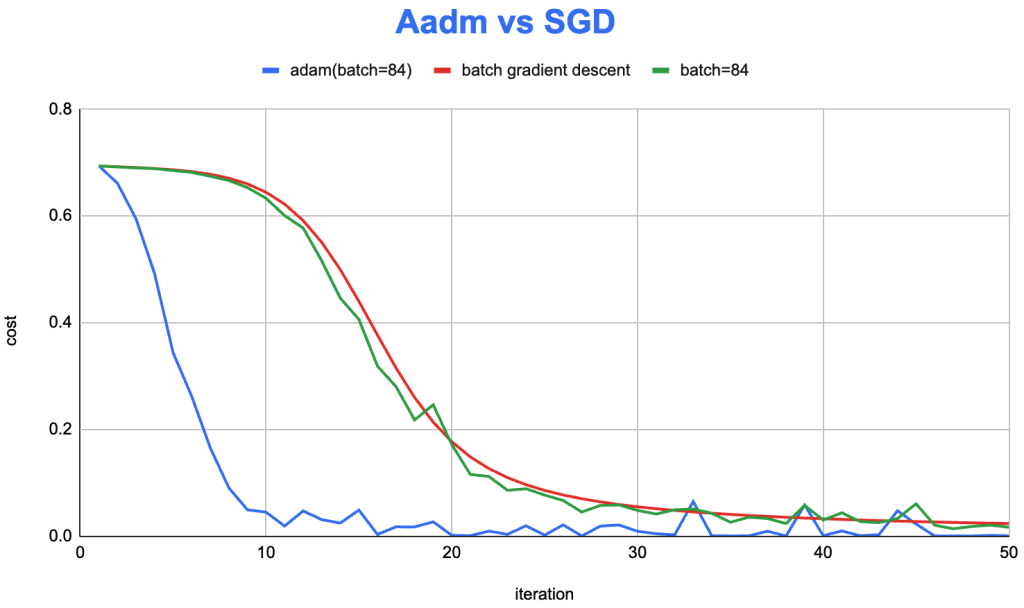
从右图可以看到,Adam(蓝色)明显的提升了迭代效率。依旧一定程度存在 mini-batch(绿色) 的梯度波动的问题。相比于,batch gradient descent (红色)算法,迭代效率大大增加,约在第10次迭代,即在第一个epoch 的第十批样本进行训练时,cost 就下降到了比较低的程度。
关于 root mean square
root mean square也叫二次平均值,考虑一组数据:\( {x_1,x_2, \cdots , x_n } \),其RMS则为:
$$ x_{rms} = \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2} = \sqrt{\frac{1}{n} (x_1^2 + x_2^2 + \cdots + x_n^2)} $$
补充说明
可以看到,所有的这些优化都是面向“最优化”问题的。梯度下降是一个一阶优化(First-order Optimization)的方法,其核心就在与每次迭代时,应该如何去更新响应的参数值,在梯度下降中也就是如何去选择合适的学习率。
牛顿法是典型的二阶优化(Second-order Optimization),在迭代时使用了二阶导数,所以,通常可以获得更好的迭代效率。但是因为二阶导数的计算复杂度会上升非常多(对应的矩阵可能是所有参数的平方,应该也有人尝试去算过了…)。这也是为什么在这个场景下,依旧是使用一阶优化方法的原因。
如果想比较好的理解学习率、Momentum、RMSprop、Adam等内容,建议先了解梯度、数值方法、最优化问题等数学方法。
到这里这个系列算是一个小阶段了,这是一个个人学习的笔记,从数学的梯度概念开始,逐步到神经网络训练的Adam优化算法,也包含部分动手实践的神经网络算法实现。完成的系列包括了:
Leave a Reply