在前述的文章（参考）中，我们实现了带有一个隐藏层的神经网络，并使用该神经网络对手写数字0/1进行识别。本文对该神经网络的识别效果以及相关的超参数的配置做一些分析与优化。

这里涉及的超参数包括了学习率、迭代次数、隐藏层神经元的个数，这里对这三个参数的不同取值进行了相关测试，并观察训练时间与模型效果。

不同学习率的模型训练

学习率应该是这里最为重要参数了。在相同的迭代次数下（这里取500），不同的学习率展现出了非常大的差异。这里从0.001开始、尝试了：0.001、0.005、0.01、0.1、0.5等取值。详细的数据如下：

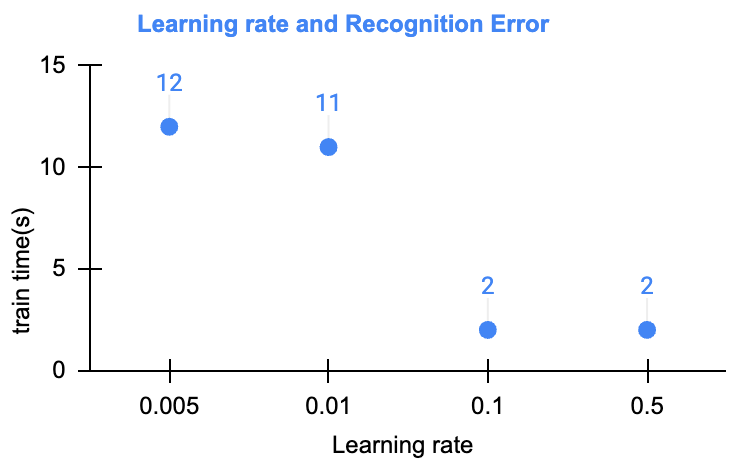
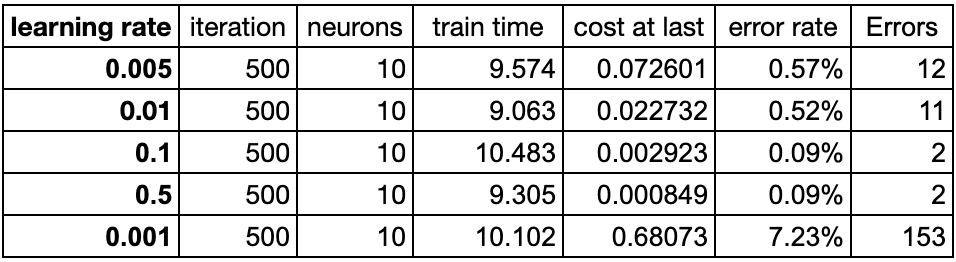
可以看到，不同的学习率展现出了训练效率的差异非常大：

• 在相同的迭代次数（均取500）情况下，学习率增加到0.1之后，预测错误率降低到了0.09%，并且再增加学习率，预测错误率并没有提升
• 在学习率，从0.001增加到了最后的0.5之后，在进行了相同的迭代次数时，训练的目标函数取值下降一直都较为明显

学习率如何影响目标函数的收敛速度

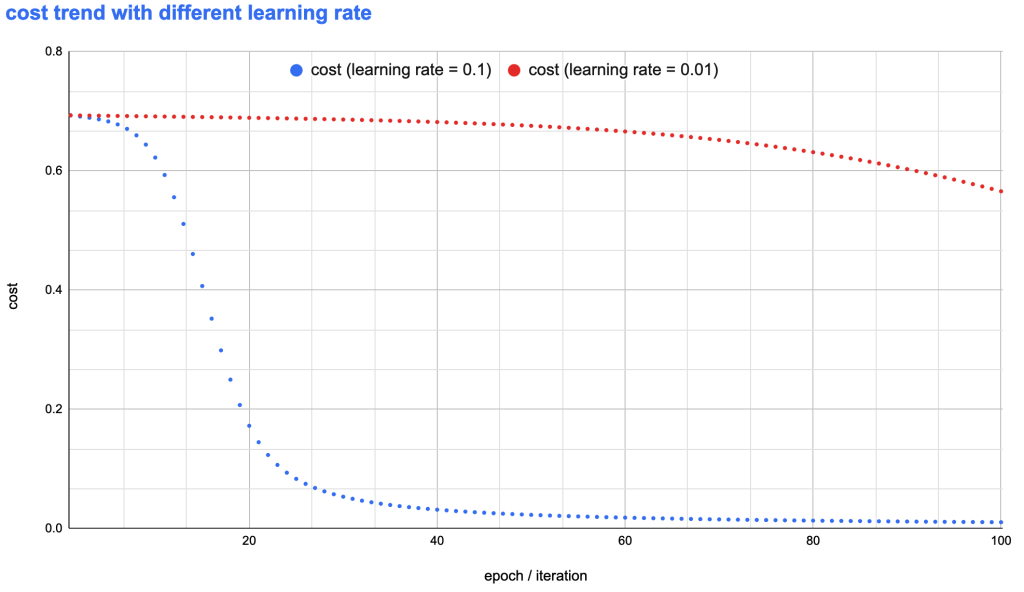
从这次实现代码也可以看到，学习率对于模型的训练效率有这至关重要的影响。如果学习率选择不合适，则会耗费大量计算资源进行非常慢的训练。那么，如果选择合适的学习率以进行更加高效进行梯度下降迭代，这是一个比较复杂的问题，这里暂时先挖个小坑在这里，待后续再做更多讨论。

迭代次数 epoch 如何影响模型

这里选取学习率为0.01，隐藏层10个人工神经元，从而观测随着“迭代次数”效率如何影响：

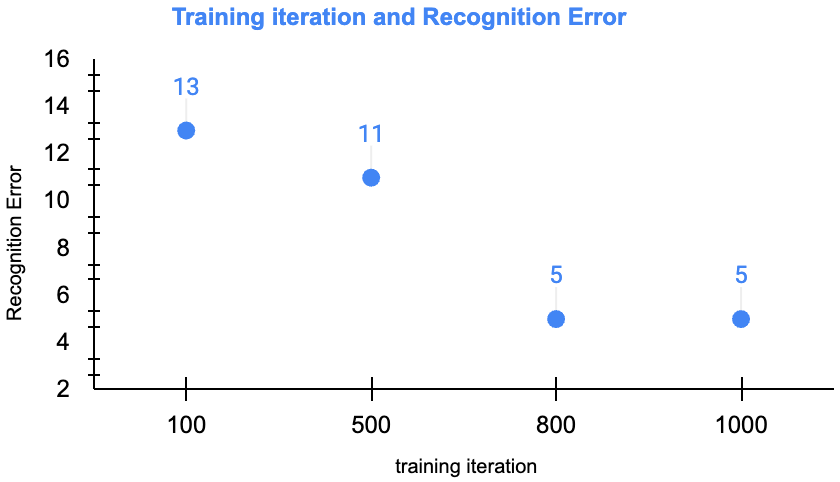
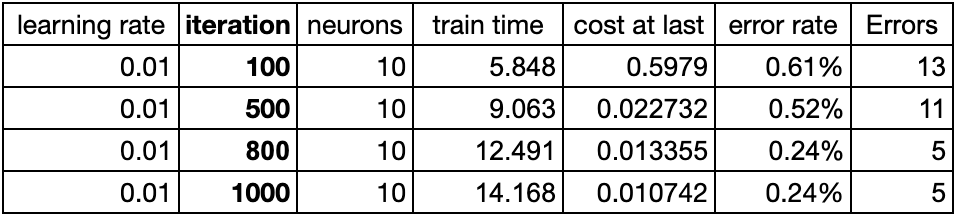
可以看到，当迭代不够充分时，目标函数收敛还不够时，模型效果也会比较差。随着迭代次数不断增加，目标函数下降就不再明显了。完整的目标函数收敛趋势如下图：

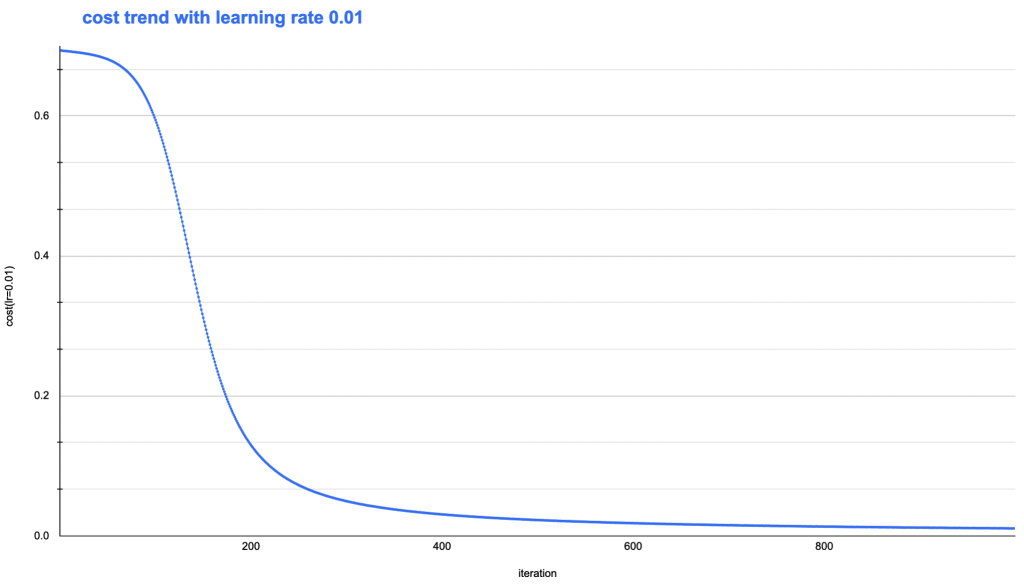
隐藏层神经元个数与模型效果

这里观察隐藏层神经元个数与模型效果趋势图。这里分别测试了1、10、50、100、150、300个神经元时候模型的表现，如下图：

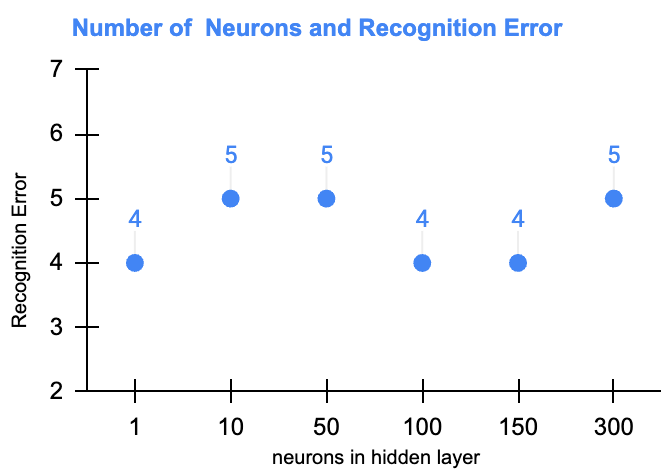
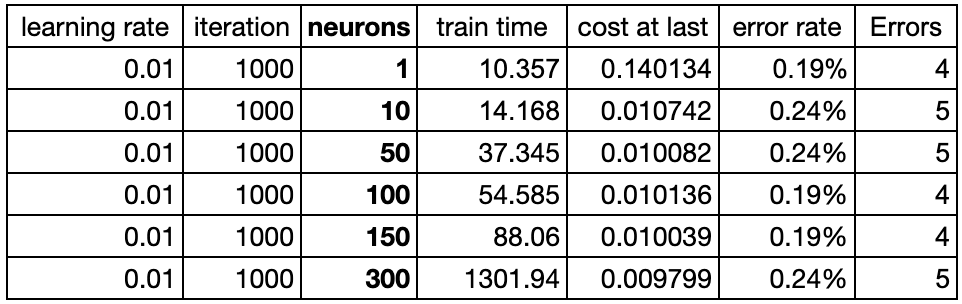
从测试来看，在这个案例中，随着隐藏层神经元个数的增加并不会提升模型性能的。这可能暗示了，此类任务（图像识别相关）使用前馈神经网络时，其性能可能较差。

部分识别失败的图片

在该模型与训练下，部分识别失败率比较高的图片如下：