梯度下降法(或者其改进算法)是机器学习的基础算法之一。在了解梯度下降算法的过程中,会经常看到一句话:“梯度是函数在某一点变化率最大的方向”。本文从较为严格数学证明的角度说明为什么是这样。理解这个证明过程,可以很好的理解梯度下降算法,及其优化算法或者优化方向。
本文主要考虑二元函数场景,即\( z=f(x,y) \)。原因是一元函数场景过于简单,不具有代表性,另外,二元场景向多元场景推广也还比较好理解。
偏导数
偏导数的定义比较好理解,即固定一个变量(当做常数),对另一个变量求导,记作:
$$ \frac{\partial z}{\partial x} \; , \; \frac{\partial z}{\partial y} $$
梯度向量
由各个偏导数组成的向量,就叫梯度向量,通常记作:\( \nabla \),有:
$$ \nabla f = (\frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} ) $$
多元/多维场景,则常记作:
$$ \nabla f = (\frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} … , \frac{\partial f}{\partial x_n} ) $$
方向导数
多元函数没有简单的“导数”的概念。但为了研究多元函数在某点的变化率,我们可以考虑“方向导数”。
具体的,考虑函数 \( z = f(x,y) \),该函数定义域为\( \mathbb{R}^2 \),其方向向量是 $$ \{ u,v | u^2 +v^2 = 1 \} $$,取其中的一个方向 \( l = (u_0,v_0) \),并假设该方向与\( x \)轴正方向夹角为\( \theta \)。
那么,函数\( z = f(x,y) \)在点\( (x_0,y_0) \)处,在方向 \( l = (u_0,v_0) \)的导数记作
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} $$
直观理解方向导数
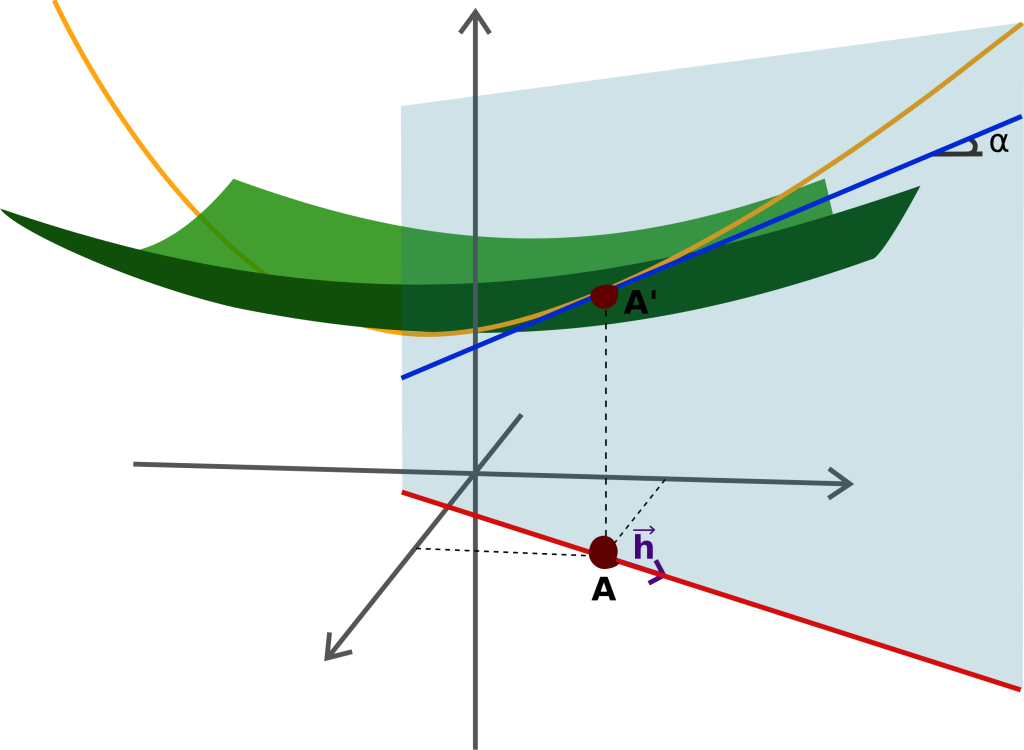
图1是一个非常清晰的关于方向导数的图例。绿色曲面即为 \( z = f(x,y) \),在点\( A^\prime \)上考虑方向为\( \vec{h}\)的方向导数。过点\( A^\prime \)与方向\( \vec{h}\),与\( z \)轴平行,存在一个平面,即图1中的半透明的平面,该平面与 \( z = f(x,y) \)相交与一条曲线,即图1中的黄色曲线。
那么,该方向导数,即为在该黄色曲线上,\( A^\prime \)位置的导数。这就是关于方向导数的直观理解。
所以,偏导数\( \frac{\partial z}{\partial x} \; , \; \frac{\partial z}{\partial y} \)可以理解为在\( (1,0) \)和\( (0,1) \)这两个方向上的方向导数。
与一般的导数定义类似的,可以定义方向导数:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \lim\limits_{P \to P_0} = \frac{f(P) – f(P_0)}{||P-P_0||} = \lim\limits_{\rho \to 0} \frac{\Delta z}{ \rho } $$
可以到如下结论(详细证明参考后续小节“方向导数的计算与证明”),如果方向\( l = (u_0,v_0) \)与 \( x \)轴的夹角是\( \theta \),那么\( z = f(x,y) \)在点\( (x_0,y_0) \)处,在方向 \( l = (u_0,v_0) \)的导数取值如下:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \frac{\partial z}{\partial x} |_{(x_0,y_0)} cos(\theta) + \frac{\partial z}{\partial y} |_{(x_0,y_0)} sin(\theta) \tag{1} $$
根据柯西不等式,我们有如下结论:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \frac{\partial z}{\partial x} |_{(x_0,y_0)} cos(\theta) + \frac{\partial z}{\partial y} |_{(x_0,y_0)} sin(\theta)
\\
\le \sqrt{ ((\frac{\partial z}{\partial x} |_{(x_0,y_0)})^2 + (\frac{\partial z}{\partial y} |_{(x_0,y_0)})^2)(sin^2(\theta)+cos^2(\theta)) }
\\
= \sqrt{ (\frac{\partial z}{\partial x} |_{(x_0,y_0)})^2 + (\frac{\partial z}{\partial y} |_{(x_0,y_0)})^2 }
$$
上面表示的极值 \( \sqrt{ (\frac{\partial z}{\partial x} |_{(x_0,y_0)})^2 + (\frac{\partial z}{\partial y} |_{(x_0,y_0)})^2 } \) 正是偏导数向量的“范数”(长度),根据柯西不等式取最大值的条件也有:
$$
\frac{cos(\theta)}{\frac{\partial z}{\partial x}} = \frac{sin(\theta)}{\frac{\partial z}{\partial y}}
\\
tan(\theta) = \frac{\frac{\partial z}{\partial y} } { \frac{\partial z}{\partial x} } = \frac{\Delta y}{\Delta x}
$$
所以,即,即当方向恰好为偏导数向量时,方向导数取最大值。也就是,我们经常会说的,会看到的,“偏导数向量是所有方向中最为陡峭的方向”或者说“梯度是函数在某一点变化率最大的方向”。
方向导数的计算与证明
在前面,我们是直接给出了如下的结论的:
$$ \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \frac{\partial z}{\partial x} |_{(x_0,y_0)} sin(\theta) + \frac{\partial z}{\partial y} |_{(x_0,y_0)} cos(\theta)$$
这个结论的获得,是需要有一些比较复杂的计算或者说证明的。这里,其主要证明步骤/方法之一,如下:
\( \frac{\partial z}{\partial l} |_{(x_0,y_0)} = \lim\limits_{P->P_0}\frac{f(P)-f(P_0)}{|P-P_0|} = \lim\limits_{P->P_0}\frac{f(x_0+\Delta{x},y_0+\Delta{y})-f(x_0,y_0)}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\)
由拉格朗日中值定理:存在\( \alpha \; \beta \),使得下式成立,且 \( 0 \le \alpha \le 1 \; and \; 0 \le \beta \le 1 \):
\(
f(x_0+\Delta{x},y_0+\Delta{y})-f(x_0,y_0)
\\
= [f(x_0+\Delta{x},y_0+\Delta{y}) – f(x_0,y_0+\Delta{y})] + [f(x_0,y_0+\Delta{y}) -f(x_0,y_0)]
\\
= f_x'(x_0 + \alpha\Delta{x} ,y_0+\Delta{y})\Delta{x} + f_y'(x_0, y_0 + \beta\Delta{y} )\Delta{y}
\)
容易有,这几个条件是等价的: \( P \to P_0 \)、\( \Delta{x} \to 0 \, and \, \Delta{y} \to 0 \) 、\( \sqrt{\Delta{x}^2+\Delta{y}^2} \to 0 \)
考虑\( \frac{\partial z}{\partial x} \)在\( (x_0,y_0)\)处连续(这是一个条件),则有: $$ \lim\limits_{\Delta{x} \to 0 \\ \Delta {y} \to 0 }f_x'(x_0 + \alpha\Delta{x} ,y_0+\Delta{y}) = f_x'(x_0,y_0) $$
故:
$$
\begin{align}
\frac{\partial z}{\partial l} |_{(x_0,y_0)} & = \lim\limits_{P->P_0}\frac{f(P)-f(P_0)}{|P-P_0|}
\\
& = \lim\limits_{P->P_0}\frac{f(x_0+\Delta{x},y_0+\Delta{y})-f(x_0,y_0)}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\\
& =\lim\limits_{P->P_0}\frac{f_x'(x_0+\alpha\Delta{x},y_0+\Delta{y})\Delta{x} + f_y'(x_0,y_0+\Delta{y})\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\\
& =\lim\limits_{P->P_0}\frac{f_x'(x_0+\alpha\Delta{x},y_0+\Delta{y})\Delta{x}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} + \frac{f_y'(x_0,y_0+\Delta{y})\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\end{align}
$$
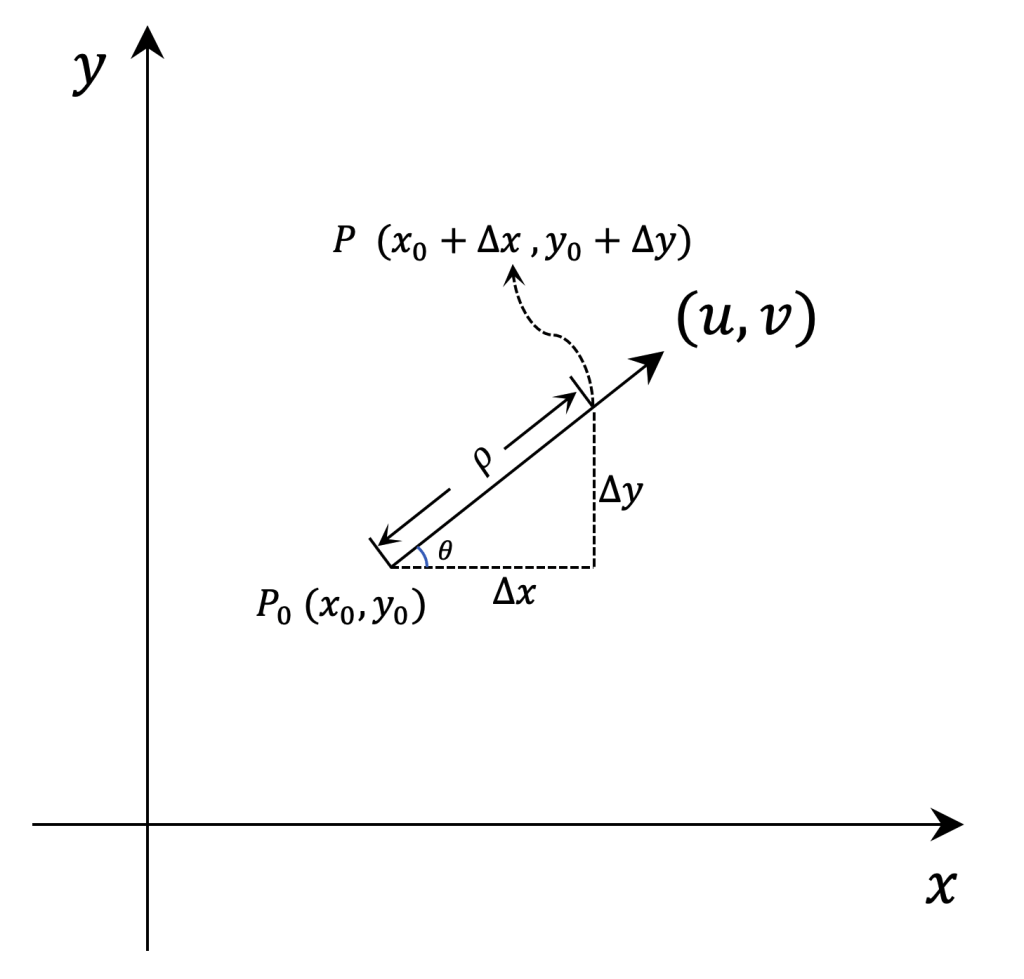
根据上面的图2,容易有:
$$
\frac{\Delta{x}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} = cos(\theta) \quad \frac{\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} = sin(\theta)
$$
所以:
\( =\lim\limits_{P->P_0}\frac{f_x'(x_0+\alpha\Delta{x},y_0+\Delta{y})\Delta{x}}{\sqrt{\Delta{x}^2+\Delta{y}^2}} + \frac{f_y'(x_0,y_0+\Delta{y})\Delta{y}}{\sqrt{\Delta{x}^2+\Delta{y}^2}}
\\
=f_x'(x_0,y_0)cos(\theta) + f_y'(x_0,y_0)sin(\theta)
\\
\)
好了,这就证明完成了。
关于上述证明
上述证明,在一般的《数学分析》教程的“多元函数微分”相关章节都会有,或者会有类似的问题证明。过程还是比较巧妙的,先是“无中生有”新增了一个项(\( f(x_0,y_0+\Delta{y}) \)),分别构造了关于 \( x \)和\( y \)的偏导数,然后使用了“中值定理”,将差值变成,导数和微分变量的积(准确的说,还要加上一个关于\( \rho \)的高阶无穷小)。
向量形式化表达
使用向量形式化表达,看起来会简洁很多。对于方向向量(这也是一个单位向量) \( \mathbf{l} = (u,v)\),函数\( f \)的偏导数向量记为\( \nabla f = (\frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} ) \) ,那么方向导数为 \( D_{\mathbf{l}}f(P_0) = \nabla f \cdot \mathbf{l} \) ,这与上面表达式的意义是相同的。
根据点击的性质,我们有:
\( D_{\mathbf{l}}f(P_0) = \nabla f \cdot \mathbf{l} = ||\nabla f|| ||\mathbf{l} || cos\theta = ||\nabla f|| cos\theta \)
从这里,更容易看出,方向向量与梯度向量相同时,方向导数取最大值,最大值即为梯度向量的模。
多维场景扩展
在很多的材料中,在前面的表达式中,经常会看到的是 \( cos(\alpha) \; cos(\beta) \),而不是本文中的 \( sin(\theta) \; cos(\theta) \)。这里的 \( \alpha \)是方向向量与x轴正方向的夹角, \( \beta \)是方向向量与y轴正方向的夹角;在定义域 \( \mathbb{R}^2 \)上有:\( \alpha + \beta = 90^{\circ} \),即有 \( cos^2\alpha + cos^2\beta = 1 \)。
这种写法有着更好的扩展性,当在更多元的情况下,例如三元场景下,即 \( z = f(x_1,x_2,x_3) \),方向向量与 x,y,z轴的夹角分别是:\( \alpha \; \beta \; \gamma \),则有: \( cos^2\alpha + cos^2\beta + cos^2 \gamma = 1 \)。
任意维度,也有类似的结论,并且应用柯西不等式时,上述结论也是类似的。
说明:直觉
本文内容需要或者可以建立如下的“直觉”:
- 在一维空间(即\( \mathbb{R}\)上的函数,在某一点上的一阶导数的符号(正/负),可以代表在该方向上,函数的趋势是增长还是下降,“正号”,则是增长;“负号”,则是下降。
- 在一维空间(即\( \mathbb{R}\)上的函数,在某一点上的一阶导数的绝对值大小,即为其“陡峭程度”(更多的时候理解为,变化率大小)
上述两个结论,基本上认为是显然的。下面扩展到多维场景,也几乎是显然的:
- 在高维空间/多维变量(即\( \mathbb{R}^n\)时,在某一点的任意方向上,都有导数,称为方向导数,该方向导数的符号(正/负),可以代表在该方向上,函数的趋势是增长还是下降,“正号”,则是增长;“负号”,则是下降。
- 在高维空间/多维变量(即\( \mathbb{R}^n\)时,在某一点的任意方向上,都有导数,该导数的绝对值大小,即为其“陡峭程度”(更多的时候理解为,变化率大小)
- 更进一步的,也就是本文中的一个结论:高维空间/多维变量(即\( \mathbb{R}^n\)时,函数的所有的方向导数,在偏导数向量方向上,取值最大,即是最为“陡峭”的方向。
所以,最后
所以,这就是为什么梯度下降算法中,总是倾向于选择偏导数向量方向进行下一次迭代。
在本科毕业后,最后留了几本书:《数学分析》(上下册)、概率论,一直到研究生毕业、再到工作都一直带着,还从北京邮寄到了杭州。本想只是做个纪念的,没想到竟然还能用上…

