知也无涯

吾生也有涯，而知也无涯，能学一点算一点…

理解大语言模型的核心：Attention

2025-12-31

admin

在整个大语言模型学习之路中，对 Attention 机制的理解大概是最为让我困惑的部分，最终经过层层解构、加上重新把“线性代数”温习了一遍之后，最终，总算某种程度的理解了 Attention 机制的设计。相信对于所有NLP专业的人，这部分都是不太容易理解的。

1. 概述
- 1.1 要构建的是直觉，而不是“推理”
2. 预处理
3. Similarity Score Matrix
- 3.1 两个“词语”的相似度
- 3.2 “Similarity Score Matrix”
4. Self-Attention
5 计算示意图
6. 注意力矩阵的观察
7. Multi-Head Attention
8. Attention 数学计算示意图
9. 全流程数学计算
10. 其他
注

1. 概述

要想讲清楚，大概也是非常不容易的，这里就做一个尝试吧。这里的重点是讲清楚 Attention Score （简称Attention）的计算。介绍的顺序是“两个词语的相似度”、“Similarity Score Matrix”、“Attention Score Matrix”。

1.1 要构建的是直觉，而不是“推理”

为什么 Attention 理解起来很难呢？我想其中有一个原因大概是这个“机制”本身并不是某种“公式推导”出来的，而是通过一篇篇论文与实践，被证明非常有效的一个机制，所以，这个机制本身的所具备的“可解释性”其实也是有限的。这大概也是，无论你在互联网上如何搜索，也没有谁可以比较简单的把这个机制说清楚的原因。但，理解这个机制构建的直觉，对于理解整个 Transformer ，以及整个当代大语言模型技术基础都是至关重要的。

2. 预处理

在“大语言模型的输入：tokenize”中详细介绍了“提示词”进入大模型处理之前，如何将提示词换行成大模型可以处理的“词向量”或者说“token embedding”。

大语言模型在开始“Attention”计算之前，还会对“token embedding”进行一些预处理，这些预处理包括了“融入”位置向量、对向量进行“归一化”处理（将各个向量都转化为均值为0、方差为1的向量，长度要统一变成1吗？）。

例如，在这里的例子中，提示词 “It’s very hot in summer. Swimming is”，先转换为embedding，然后加上位置编码（positional encoder)、再进行正规化，最后变换为如下的向量 “ X ” ：

|-------------------------------------------------------------------------------------------------------------------------------------------
|  Token    | wte[:3] (word token embedding)  | wpe[:3](word positional e..)|   wte [:3]  + wpe [:3]     | X[:3] (Norm)                    |
|-------------------------------------------------------------------------------------------------------------------------------------------
|It         | [0.039,   -0.0869, 0.0662 ,...] | [-0.0188, -0.1974, 0.004  ] | [0.0202, -0.2844,0.0702 ]  | [ 0.0129, -0.1104, -0.0317,...] |
|âĢ         | [-0.075,  0.0948,  -0.0034,...] | [0.024,   -0.0538, -0.0949] | [-0.051, 0.041,  -0.0982]  | [-0.0530,  0.0588, -0.1290,...] |
|Ļ          | [-0.0223, 0.0182,  0.2631 ,...] | [0.0042,  -0.0848, 0.0545 ] | [-0.0181,-0.0666,0.3176 ]  | [-0.0170, -0.0242,  0.1639,...] |
|s          | [-0.064,  -0.0469, 0.2061 ,...] | [-0.0003, -0.0738, 0.1055 ] | [-0.0643,-0.1207,0.3116 ]  | [-0.0754, -0.0842,  0.1842,...] |
|Ġvery      | [-0.0553, -0.0348, 0.0606 ,...] | [0.0076,  -0.0251, 0.127  ] | [-0.0477,-0.0599,0.1876 ]  | [-0.0566, -0.0280,  0.0953,...] |
|Ġhot       | [0.0399,  -0.0053, 0.0742 ,...] | [0.0096,  -0.0339, 0.1312 ] | [0.0495, -0.0392,0.2054 ]  | [ 0.0587, -0.0086,  0.1073,...] |
|Ġin        | [-0.0337, 0.0108,  0.0293 ,...] | [0.0027,  -0.0205, 0.1196 ] | [-0.031, -0.0098,0.149  ]  | [-0.0391,  0.0209,  0.0731,...] |
|Ġsummer    | [0.0422,  0.0138,  -0.0213,...] | [0.0025,  -0.0032, 0.1174 ] | [0.0448, 0.0106, 0.0961 ]  | [ 0.0532,  0.0397,  0.0181,...] |
|.          | [0.0466,  -0.0113, 0.0283 ,...] | [-0.0012, -0.0018, 0.111  ] | [0.0454, -0.0131,0.1394 ]  | [ 0.0553,  0.0152,  0.0579,...] |
|ĠSw        | [0.0617,  0.0373,  0.1018 ,...] | [0.0049,  0.0021,  0.1178 ] | [0.0666, 0.0395, 0.2196 ]  | [ 0.0807,  0.0691,  0.1216,...] |
|imming     | [-0.1385, -0.1774, -0.0181,...] | [0.0016,  0.0062,  0.1004 ] | [-0.1369,-0.1711,0.0823 ]  | [-0.1528, -0.1249, -0.0017,...] |
|Ġis        | [-0.0097, 0.0101,  0.0556 ,...] | [-0.0036, 0.0175,  0.1068 ] | [-0.0133,0.0275, 0.1623 ]  | [-0.0175,  0.0605,  0.0880,...] |
|-------------------------------------------------------------------------------------------------------------------------------------------

这里的 “X” 是一个由12个 “token embedding”组成的矩阵，“形状”是 12 x 768 。在数学符号上，有：

   ---------------------------------------    ------------------------------------------   -------------
   |     [ 0.0129, -0.1104, -0.0317,...] |    | x_1  = [ 0.0129, -0.1104, -0.0317,...] |   |It         |
   |     [-0.0530,  0.0588, -0.1290,...] |    | x_2  = [-0.0530,  0.0588, -0.1290,...] |   |âĢ         |
   |     [-0.0170, -0.0242,  0.1639,...] |    | x_3  = [-0.0170, -0.0242,  0.1639,...] |   |Ļ          |
   |     [-0.0754, -0.0842,  0.1842,...] |    | x_4  = [-0.0754, -0.0842,  0.1842,...] |   |s          |
   |     [-0.0566, -0.0280,  0.0953,...] |    | x_5  = [-0.0566, -0.0280,  0.0953,...] |   |Ġvery      |
   | X = [ 0.0587, -0.0086,  0.1073,...] |    | x_6  = [ 0.0587, -0.0086,  0.1073,...] |   |Ġhot       |
   |     [-0.0391,  0.0209,  0.0731,...] |    | x_7  = [-0.0391,  0.0209,  0.0731,...] |   |Ġin        |
   |     [ 0.0532,  0.0397,  0.0181,...] |    | x_8  = [ 0.0532,  0.0397,  0.0181,...] |   |Ġsummer    |
   |     [ 0.0553,  0.0152,  0.0579,...] |    | x_9  = [ 0.0553,  0.0152,  0.0579,...] |   |.          |
   |     [ 0.0807,  0.0691,  0.1216,...] |    | x_10 = [ 0.0807,  0.0691,  0.1216,...] |   |ĠSw        |
   |     [-0.1528, -0.1249, -0.0017,...] |    | x_11 = [-0.1528, -0.1249, -0.0017,...] |   |imming     |
   |     [-0.0175,  0.0605,  0.0880,...] |    | x_12 = [-0.0175,  0.0605,  0.0880,...] |   |Ġis        |
   ---------------------------------------    ------------------------------------------   -------------

3. Similarity Score Matrix

在正式介绍 Attention 之前，为了能够比较好的理解“为什么”是这样，这里先引入了“Similarity”的概念，最终在该概念上，新增权重矩阵，就是最终的 Attention ：

$$ \text{Similarity} = \text{softmax}(\frac{XX^{T}}{\sqrt{d}})X $$

这里删除了参数矩阵：$W^Q \quad W^K \quad W^V $

$$ \text{Attention} = \text{softmax}(\frac{QK^{T}}{\sqrt{d}})V $$

其中， $Q = XW^Q \quad K = XW^K \quad V = XW^V $

3.1 两个“词语”的相似度

在向量为单位长度的时候，通常可以直接使用“内积”作为两个向量的相似度度量。例如，考虑词语 “hot” 与 “summer” 的相似度，则可以“简化”的处理这两个词（Token）的向量的“内积”。

在前面的文章“大语言模型的输入：tokenize”中，较为详细的介绍了大语言模型如何把一个句子转换成一个的 Token，然后再转换为一个个“向量”。那么，我们通常会通过两个向量的余弦相似度来描述其相似度，如果向量的“长度”（$L_2 $ 范数）是单位长度，那么也通常会直接使用“内积”描述两个向量的相似度：

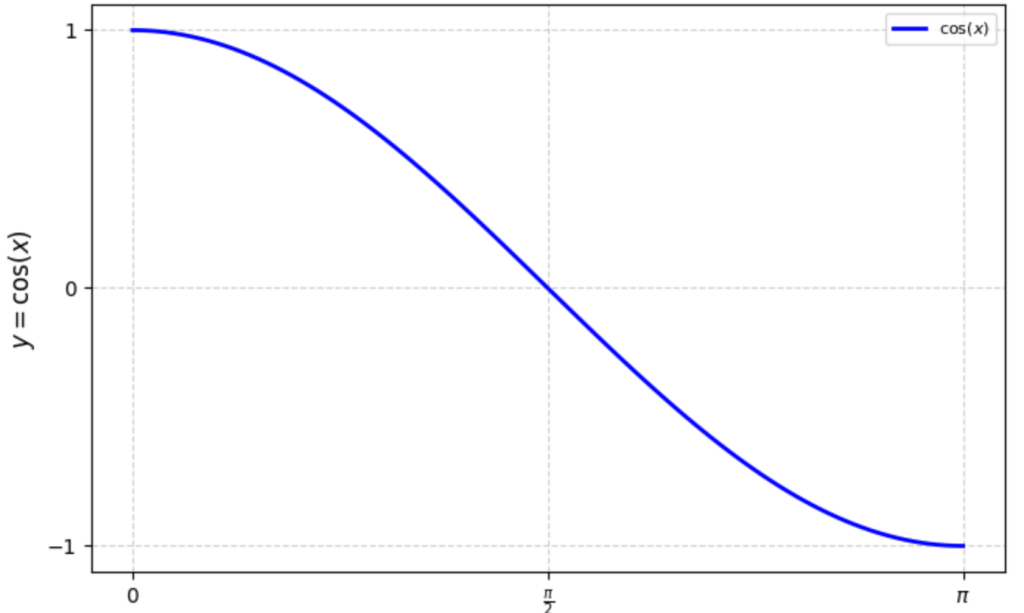
$$
\cos \theta = \frac{\alpha \cdot \beta}{\|\alpha\| \|\beta\| }
$$

$f(x) = \cos(x) $ 的图像如右图，故：

夹角为 0 时，最为相似，这时候 $\cos(x) = 1 $
夹角 $\pi $ 时，最“不”相似，这时候 $\cos(x) = 0 $

例如，

3.2 “Similarity Score Matrix”

因为两个向量的“内积”某种程度可以表示为相似度。那么，对于句子中的某个 token 来说，与其他所有向量各自计算“内积”，就可以获得一个与其他所有向量“相似程度”的数组，再对这个数组进行 softmax 计算就可以获得一个该 token 与其他所有向量“相似程度”的归一化数组。这个归一化的数据，就可以理解为这里的“Similarity Score Matrix”。

这里依旧以“大语言模型的输入：tokenize”示例中的句子为演示示例。

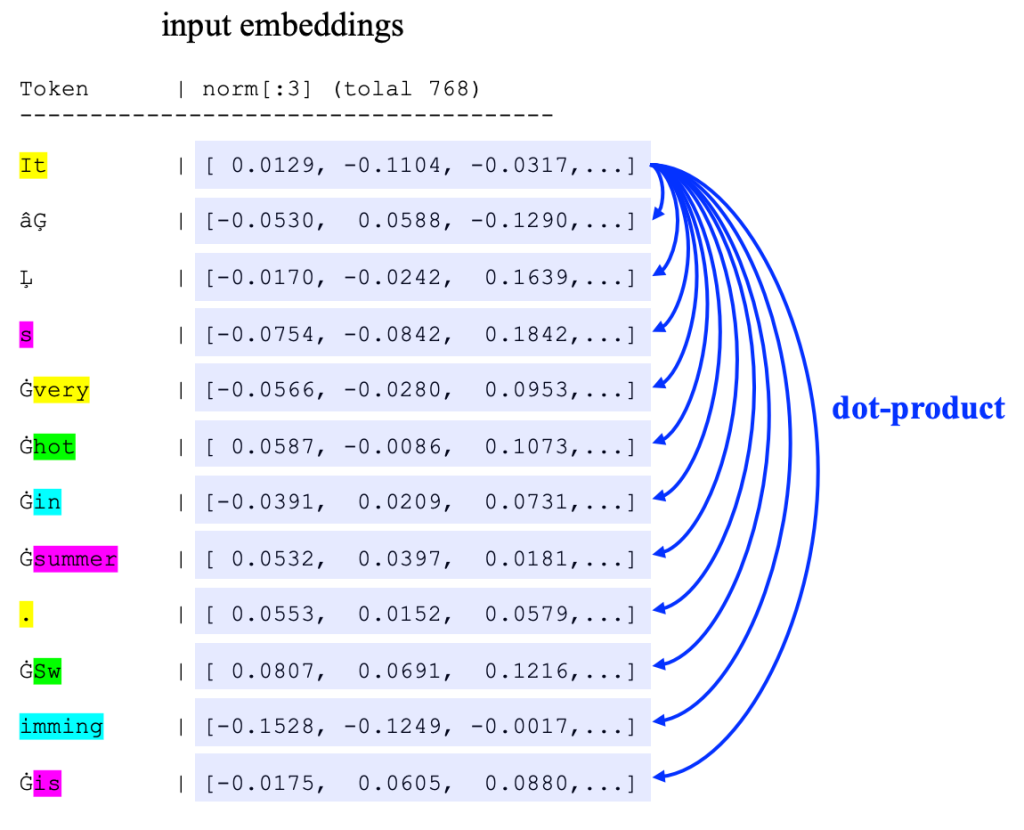
更为具体的，可以参考右图。这里考虑 Token “It” 与其他所有词语的相似度。即计算 Token “It” 的 Embedding 向量，与其他所有向量的“内积”。

更进一步，如果计算两两词语之间的相似度，并进行归一化（softmax ），则有如下的Similarity Matrix：

[0.6975, 0.0347, 0.0236, 0.0298, 0.0386, 0.0282, 0.0272, 0.0270, 0.0216, 0.0244, 0.0219, 0.0254]
[0.0000, 0.9994, 0.0002, 0.0000, 0.0000, 0.0001, 0.0000, 0.0000, 0.0000, 0.0001, 0.0001, 0.0000]
[0.0000, 0.0004, 0.9987, 0.0001, 0.0001, 0.0001, 0.0000, 0.0002, 0.0000, 0.0001, 0.0002, 0.0000]
[0.0002, 0.0003, 0.0004, 0.9945, 0.0008, 0.0004, 0.0011, 0.0003, 0.0007, 0.0005, 0.0002, 0.0007]
[0.0013, 0.0012, 0.0013, 0.0042, 0.9724, 0.0044, 0.0047, 0.0021, 0.0030, 0.0013, 0.0012, 0.0028]
[0.0002, 0.0003, 0.0003, 0.0004, 0.0009, 0.9932, 0.0005, 0.0020, 0.0004, 0.0009, 0.0006, 0.0003]
[0.0049, 0.0048, 0.0038, 0.0299, 0.0258, 0.0125, 0.7728, 0.0086, 0.0779, 0.0095, 0.0025, 0.0471]
[0.0001, 0.0001, 0.0005, 0.0002, 0.0003, 0.0015, 0.0002, 0.9959, 0.0002, 0.0003, 0.0003, 0.0002]
[0.0049, 0.0048, 0.0045, 0.0255, 0.0203, 0.0126, 0.0974, 0.0082, 0.7698, 0.0094, 0.0024, 0.0401]
[0.0001, 0.0001, 0.0001, 0.0002, 0.0001, 0.0003, 0.0001, 0.0002, 0.0001, 0.9983, 0.0002, 0.0002]
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.9998, 0.0000]
[0.0033, 0.0027, 0.0028, 0.0129, 0.0110, 0.0063, 0.0334, 0.0055, 0.0228, 0.0075, 0.0025, 0.8893]

在这个示例中，则会有上述 12×12 的矩阵。该矩阵反应了“词”与“词”之间的相似度。如果，我们把每一行再进行一个“归一化”（注右图已经经过了归一化），那么每一行，就反应了一个词语与其他所有词语相似程度的一个度量。

例如，右图中 it 可能与 very 最为相似（除了自身）。

4. Self-Attention

4.1 对比

注意到最终的 “Attention” 计算公式和上述的“Similarity Score Matrix”的差别就是参数矩阵W：

$$ \text{Similarity Score} = \text{softmax}(\frac{XX^{T}}{\sqrt{d}})X $$

这里没有参数矩阵：$W^Q \quad W^K \quad W^V $

$$ \text{Attention} = \text{softmax}(\frac{QK^{T}}{\sqrt{d}})V $$

其中， $Q = XW^Q \quad K = XW^K \quad V = XW^V $

4.2 为什么需要参数矩阵 W

那么，为什么需要 $W^Q \,, W^K \,, W^V $ 呢？这三个参数矩阵乘法，意味着什么呢？要说清楚、要理解这个点并不容易，也没有什么简单的描述可以说清楚的，这也大概是为什么，对于非 NLP 专业的人，要想真正理解 Transformer 或 Attention 是比较困难的。

你可能会看到过一种比较普遍的、简化版本，大概是说 $W^Q $ 是一个 Query 矩阵，表示要查询什么；$W^K $ 是一个 Key 矩阵，表示一个词有什么。这个说法似乎并不能增加对上述公式的理解。

那么，一个向量乘以一个矩阵时，这个“矩阵”意味着什么？是的，就是“线性变换”。

4.3 线性变换 Linear Transformations

一般来说，$W^Q \,, W^K \,, W^V $ 是一个 $d \times d $ 的矩阵^[1]。对于的 Token Embedding （上述的矩阵 X ）所在的向量空间，那么 $W^Q \,, W^K \,, W^V $ 就是该向量空间的三个“线性变换”。

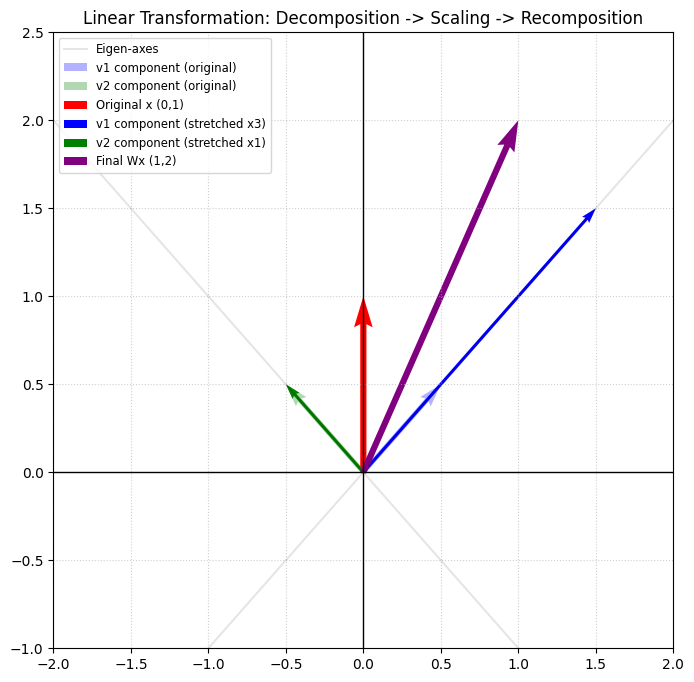
那么线性变换对于向量空间的作用是什么呢？这里我们以“奇异值分解”的角度来理解这个问题^[2]，即对向量进行拉伸/压缩、旋转、镜像变换。$W^Q \,, W^K \,, W^V $ 则会分别对向量空间的向量（即Token Embedding）做类似的变换。变换的结果即为：

$$ Q = XW^Q \quad \quad K = XW^K \quad \quad V = XW^V $$

那么，如果参数矩阵“设计”合理，“Token”与“Token”之间就可以建立“期望”的 Attention 关系，例如：“代词”（it），总是更多的关注于“名词”；“名词”更多的关注与附近的“形容词”；再比如，“动词”更多关注前后的“名词”等。除了词性，线性变换关注的“维度”可能有很多，例如“位置”、“情感”、“动物”、“植物”、“积极/消极”等。关于如何理解 token embedding 的各个“维度”含义可以参考：Word Embedding 的可解释性探索。

当然，这三个参数矩阵都不是“设计”出来的，而是“训练”出来的。所以，要想寻找上述如此清晰的“可解释性”并不容易。2019年的论文《What Does BERT Look At? An Analysis of BERT’s Attention》较为系统的讨论了这个问题，感兴趣的可以去看看。

关于线性变换如何作用在向量空间上，可以参考：线性代数、奇异值分解–深度学习的数学基础。

所以，$ \frac{QK^T}{\sqrt{d}} = \frac{XW^Q (XW^K)^T}{\sqrt{d}} $ 则可以系统的表示，每个“Token”对于其他“Token”的关注程度（即pay attention的程度）。可以注意到：

增加了参数矩阵$W^Q \,, W^K \,, W^V $后，前面的“相似性”矩阵，就变为“注意力”矩阵
“Token” 之间的关注程度不是对称的。例如 Token A 可能很关注 B；但是 B 可能并不关注 A
这里的 $\sqrt{d} $ 根据论文描述，可以提升计算性能；

如果，你恰好理解了上面所有的描述，大概会有点失望的。就只能到这儿吗？似乎就只能到这里了。如果，你有更深刻的理解，欢迎留言讨论。

接下里，我们来看看 “Attention Score Matrix” 的计算。

4.4 Attention Score Matrix

使用上述的 “Similarity Score Matrix” 的计算方式，可以计算类似的 “Attention Score Matrix”，之后再对该矩阵进行 softmax 计算就可以获得每个词语对于其他所有词语的 Attention Score，或者叫“关注程度”。有了这个关注程度，再乘以 V 矩阵，原来的 Token Embedding 就变换为一个新的带有上下文的含义的 Token Eembedding 了，即 Context Embedding^[3]。

类似的，我们有右图的 Attention Score Matrix 计算。

该矩阵反应了两个 Token 之间的 Attention 关系。该关系，通过对经过线性变换的 Token Embedding ，再进行内积计算获得。

           Attention Score Matrix (12 x 12)
           It     âĢ     Ļ      s    Ġvery  Ġhot   Ġin   Ġsummer   .     ĠSw   imming  Ġis
         -----------------------------------------------------------------------------------
 It      [ 0.14, -1.53, -1.45, -1.71, -1.69, -1.74, -2.36, -2.27, -2.37, -1.33, -0.58, -2.40]  |
 âĢ      [ 0.70, -0.93, -1.72, -1.02, -1.52, -2.24, -1.90, -2.19, -1.63, -2.13, -1.66, -2.14]  |
 Ļ       [-0.60, -1.81, -1.99, -1.96, -2.57, -1.84, -1.62, -2.04, -0.98, -1.18, -2.23, -2.25]  |
 s       [-0.46, -1.33, -1.60, -2.65, -2.24, -1.99, -2.89, -1.44, -2.05, -2.77, -2.09, -2.74]  |
 Ġvery   [ 0.29, -1.42, -1.77, -1.15, -0.94, -1.14, -1.81, -1.04, -1.77, -2.13, -0.60, -0.82]  |
 Ġhot    [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10, -0.95, -0.14, -1.32, -0.57,  0.06, -1.07]  12
 Ġin     [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41, -1.69, -2.74, -1.89, -1.17, -2.02]  rows
 Ġsummer [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11, -1.51, -1.15, -1.45, -1.20]  |
 .       [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42, -2.73, -1.82, -3.21]  |
 ĠSw     [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29, -0.43, -1.51]  |
 imming  [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15, -1.08]  |
 Ġis     [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99]  |
         -----------------------------------------------------------------------------------
         |<----------------------------- columns: 12 -------------------------------------->|

4.5 Masked Attention Score Matrix

上述计算，是一个典型的 Self Attention 计算过程，BERT 模型就使用类似的计算，但 GPT 模型（或者叫 Decoder 模型）还有一些不同。GPT 模型中为了训练出更好的从现有 Token 中生成新 Token 的模型，将上述的 Self Attention 更改成了 Masked Self Attention ，即将 Attention Score Matrix 的右上角部分全部置为 -inf （即负无穷），后续经过 softmax 之后这些值都会变成零，即，在该类模型下，一个词语对于其后面的词的关注度为 0 。

在 Decoder 模型设计中，为了生成更准确的下一个 Token 所以在训练和推理中，仅会计算Token 对之前的 Token 的 Attention ，所以上述的矩阵的右上角部分就会被遮盖，即就是右侧的 “Masked Attention Score Matrix”。

           Masked Attention Score Matrix (12 x 12)
           It     âĢ     Ļ      s    Ġvery  Ġhot   Ġin   Ġsummer   .     ĠSw   imming  Ġis
         ---------------------------------------------------------------------------------------
 It      [ 0.14,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]  |
 âĢ      [ 0.70, -0.93,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]  |
 Ļ       [-0.60, -1.81, -1.99,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]  |
 s       [-0.46, -1.33, -1.60, -2.65,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]  |
 Ġvery   [ 0.29, -1.42, -1.77, -1.15, -0.94,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]  |
 Ġhot    [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]  12
 Ġin     [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41,  -inf,  -inf,  -inf,  -inf,  -inf]  rows
 Ġsummer [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11,  -inf,  -inf,  -inf,  -inf]  |
 .       [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42,  -inf,  -inf,  -inf]  |
 ĠSw     [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29,  -inf,  -inf]  |
 imming  [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15,  -inf]  |
 Ġis     [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99]  |
         ---------------------------------------------------------------------------------------
         |<----------------------------- columns: 12 -------------------------------------->|

通常为了快速计算对于上述的计算值会除以 $\sqrt{d} $ ，可以提升计算的效率。

4.6 归一化(softmax) Attention Score

对于上述矩阵的每一行都进行一个 softmax 计算，就可以获得一个归一化的按照百分比分配的Attention Score。

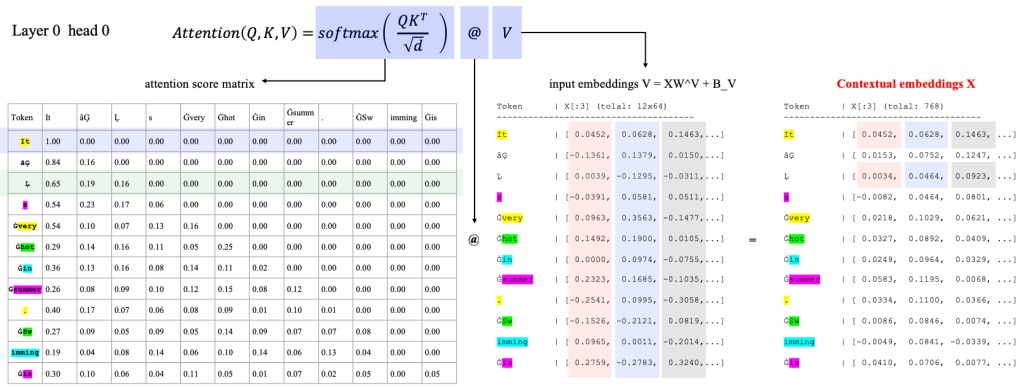
经过归一化之后，每个词语对于其他词语的 Attention 程度都可以使用百分比表达处理。例如，“summer”对于“It”的关注程度最高，为26%；其次是关注“hot”，为15%。可以看到这一组线性变换（$W^Q\,W^K $）对于第一个位置表达特别的关注。

           The Attention Score Matrix (12 x 12)
           It   âĢ    Ļ     s     Ġvery  Ġhot  Ġin  Ġsummer  .   ĠSw   imming Ġis
         -----------------------------------------------------------------------------
 It      [1.00  0.00  0.00  0.00   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]  |
 âĢ      [0.84  0.16  0.00  0.00   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]  |
 Ļ       [0.65  0.19  0.16  0.00   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]  |
 s       [0.54  0.23  0.17  0.06   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]  |
 Ġvery   [0.54  0.10  0.07  0.13   0.16  0.00  0.00  0.00  0.00  0.00  0.00  0.00]  |
 Ġhot    [0.29  0.14  0.16  0.11   0.05  0.25  0.00  0.00  0.00  0.00  0.00  0.00]  12
 Ġin     [0.36  0.13  0.16  0.08   0.14  0.11  0.02  0.00  0.00  0.00  0.00  0.00]  rows
 Ġsummer [0.26  0.08  0.09  0.10   0.12  0.15  0.08  0.12  0.00  0.00  0.00  0.00]  |
 .       [0.40  0.17  0.07  0.06   0.08  0.09  0.01  0.10  0.01  0.00  0.00  0.00]  |
 ĠSw     [0.27  0.09  0.05  0.09   0.05  0.14  0.09  0.07  0.07  0.08  0.00  0.00]  |
 imming  [0.19  0.04  0.08  0.14   0.06  0.10  0.14  0.06  0.13  0.04  0.02  0.00]  |
 Ġis     [0.30  0.10  0.06  0.04   0.11  0.05  0.01  0.07  0.02  0.05  0.12  0.04]  |
         -----------------------------------------------------------------------------
         |<----------------------------- columns: 12 --------------------------->|

4.7 Contextual Embeddings

最后，再按照上述的 Attention Matrix 的比例，将各个 Token Embedding 进行一个“加权平均计算”。

例如，上述的加权计算时，“summer” 则会融入 26% 的“It”，15%的“hot”… ，最后生成新的 “summer” 的表达，这个表达也可以某种程度理解为 “Contextual Embeddings”。需要注意的是，这里在计算加权平均，也不是直接使用原始的 Token Embedding ，也是一个经过了线性变换的Embedding，该线性变换矩阵也是经过训练而来的，即矩阵 $W^V $。

例如，上述的加权计算时，“summer” 则会融入 26% 的“It”，15%的“hot”… ，最后生成新的 “summer” 的表达，这个表达也可以某种程度理解为 “Contextual Embeddings”。

需要注意的是，这里在计算加权平均，也不是直接使用原始的 Token Embedding ，也是一个经过了线性变换的Embedding，该线性变换矩阵也是经过训练而来的，即矩阵 $W^V $。

Token      | Contextual Embeddings(12 x 768)
--------------------------------------------
It         | [ 0.0452,  0.0628,  0.1463,...]
âĢ         | [ 0.0153,  0.0752,  0.1247,...]
Ļ          | [ 0.0034,  0.0464,  0.0923,...]
s          | [-0.0082,  0.0464,  0.0801,...]
Ġvery      | [ 0.0218,  0.1029,  0.0621,...]
Ġhot       | [ 0.0327,  0.0892,  0.0409,...]
Ġin        | [ 0.0249,  0.0964,  0.0329,...]
Ġsummer    | [ 0.0583,  0.1195,  0.0068,...]
.          | [ 0.0334,  0.1100,  0.0366,...]
ĠSw        | [ 0.0086,  0.0846,  0.0074,...]
imming     | [-0.0049,  0.0841, -0.0339,...]
Ġis        | [ 0.0410,  0.0706,  0.0077,...]

5 计算示意图

如下的示意图，一定的可视化的表达了，一个 Token 如何经过上述的矩阵运算，如何了其他 Token 的内容。

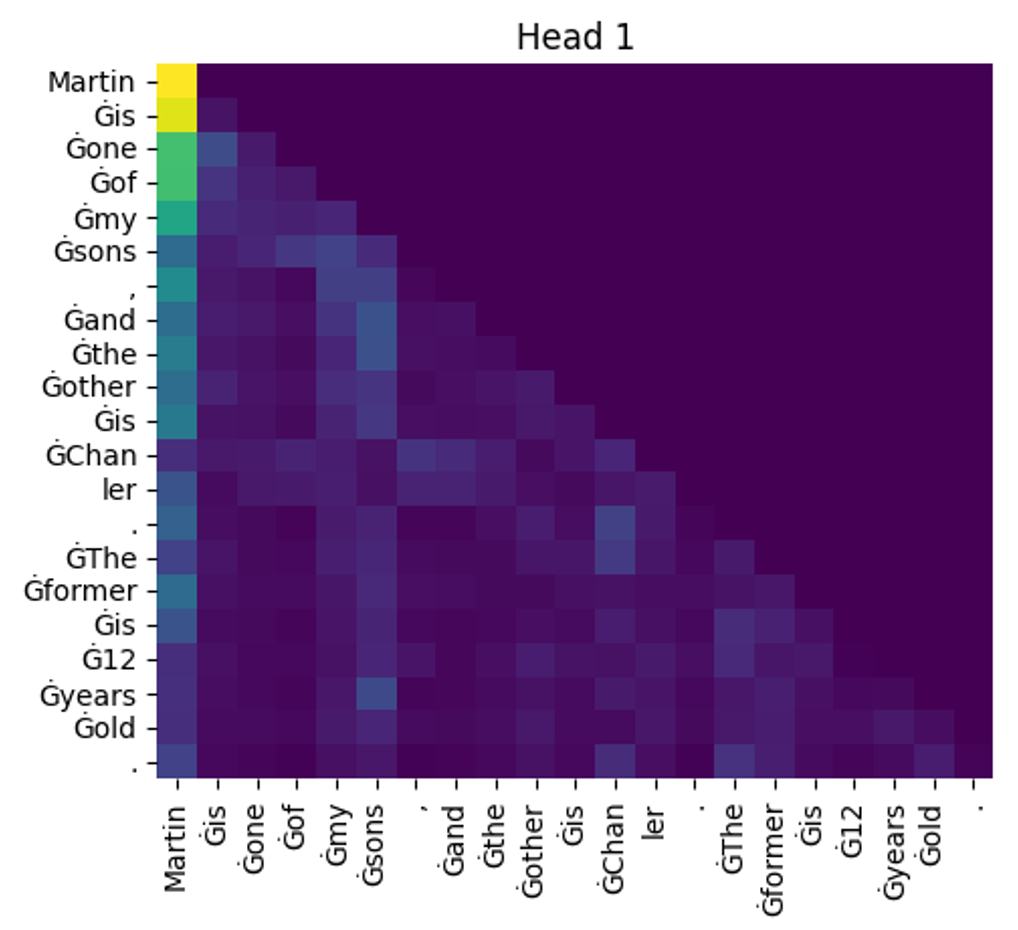
6. 注意力矩阵的观察

那么，我们给定于如下的提示词输入：“Martin’s one of my sons, and the other is Chanler.”。看看在 GPT 模型中，各个Token之间的 Attention 情况：

这句话总计有21个token，所以这是一个21×21的矩阵
这里是“masked self-attention”，所以矩阵的右上半区都是 “0” 。
在GPT2中，一共12层，每层12个“头”，所以一共有“144”个类似的矩阵
$W^Q \,, W^K \,, W^V $ 的维度都是768×64，所以粗略的估计这部分的参数量就超过2000万，具体的：

768*64*3*144 = 21,233,664

7. Multi-Head Attention

7.1 Scaled Dot-Product Attention

以前面小结“预处理”中的 X 为例，Attention Score Matrix 就有如下的计算公式：

$$
\begin{aligned}
\text{Attention Score Matrix} & = \text{softmax}(\frac{QK^T}{\sqrt{d}}) \\
& = \text{softmax}(\frac{XW^Q(XW^K)^T}{\sqrt{d}})
\end{aligned}
$$

最终的 Attention 计算如下：

$$
\begin{aligned}
\text{Attention}(Q,K,V) & = \text{softmax}(\frac{QK^T}{\sqrt{d}})V \\
& = \text{softmax}(\frac{XW^Q(XW^K)^T}{\sqrt{d}})XW^V
\end{aligned}
$$

7.2 Multi-Head Attention

上述的“Attention”在论文“Attention Is All You Need”称为“Scaled Dot-Product Attention”。更进一步的在论文中提出了“Multi-Head Attention”（经常被缩写为“MHA”）。对应的公式如下（来自原始论文）：

$$
\begin{aligned}
\text{MultiHead}(Q, K, V) & = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O \\
\text{where} \quad \text{head}_i & = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
\end{aligned}
$$

更完整的解释，可以参考原始论文。这里依旧以前文的示例来说明什么是MHA。

在本文第4章“Self-Attention”中，较为详细的介绍了相关的计算（即模型的推理过程）。在示例中，一共有12个“Token”，在进入 Attention 计算时经过位置编码、正则化后，12个“Token”向量组成矩阵“X”，这里的“X”的 shape 为 12 x 768，通常使用符号 $l \times d $ 或者 $l \times d_{model} $ 表示。最终输出的 Contextual Embedding 也是 $l \times d_{model} $ 的一组表示12个 Token 向量，这是每个向量相比最初的输入向量，则融合上下文中其他词语的含义。在一个多层的模型中，这组向量则可以作为下一层的输入。

在“Multi-Head Attention”其输入、输出与“Self-Attention”一样，都是 $l \times d_{model} $ 。但是，对于最终输出的 $l \times d_{model} $ 的向量/矩阵，在 MHA 中则分为多个 HEAD 各自计算其中的一部分，例如，一共有 $d_{model} $ 列，那么则分别有 $h $ 个HEAD，每个 HEAD 输出其中的 $\frac{d_{model}}{h} $ 列。在上述示例中，供有12个HEAD，即 $h=12 $，模型维度为768，即$d_{model} = 768 $，所以每个HEAD，最终输出 $64 = \frac{d_model}{h} = \frac{768}{12} $ 列。即：

$$
\begin{aligned}
\text{where} \quad \text{head}_i & = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)
\end{aligned}
$$

然后由12个 Head 共同组成（concat）要输出的 Contextual Embedding，并对此输出做了一个线性变换$W^O $。即：

$$
\begin{aligned}
\text{MultiHead}(Q, K, V) & = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O
\end{aligned}
$$

7.3 Self Attention vs MHA

Self Attention

Multi Head Attention

7.4 Multi-Head Attention 小结

“Multi-Head Attention” 与经典“Attention” 有着类似的效果，但是有着更好的表现性能
“Multi-Head Attention” 与经典“Attention” 有相同的输入，相同的输出

8. Attention 数学计算示意图

如下的图片，半可视化的展示了在GTP2中，某一个HEAD中Attention的计算。

9. 全流程数学计算

完整的计算，就是一个“forward propagation”或者叫“inference”的过程，这里依旧以上述的提示词“It’s very hot in summer. Swimming is”，并观察该提示词在 GPT2 模型中的第一个Layer、第一个Head中的计算。完成的代码可以参考：Attention-Please.ipynb

9.1 Token Embedding 和 Positional Embedding

Token Embedding

Positional Embedding

|------------  -----------------------------------     -------------------------------     ------------------------------
|  Token    |  | wte[:3] (word token embedding)  |     | wpe[:3](word positional e..)|     |   wte [:3]  + wpe [:3]     |
|------------  -----------------------------------     -------------------------------     ------------------------------
|It         |  | [0.039,   -0.0869, 0.0662 ,...] |     | [-0.0188, -0.1974, 0.004  ] |     | [0.0202, -0.2844,0.0702 ]  |
|âĢ         |  | [-0.075,  0.0948,  -0.0034,...] |     | [0.024,   -0.0538, -0.0949] |     | [-0.051, 0.041,  -0.0982]  |
|Ļ          |  | [-0.0223, 0.0182,  0.2631 ,...] |     | [0.0042,  -0.0848, 0.0545 ] |     | [-0.0181,-0.0666,0.3176 ]  |
|s          |  | [-0.064,  -0.0469, 0.2061 ,...] |     | [-0.0003, -0.0738, 0.1055 ] |     | [-0.0643,-0.1207,0.3116 ]  |
|Ġvery      |  | [-0.0553, -0.0348, 0.0606 ,...] |  +  | [0.0076,  -0.0251, 0.127  ] |  =  | [-0.0477,-0.0599,0.1876 ]  |
|Ġhot       |  | [0.0399,  -0.0053, 0.0742 ,...] |     | [0.0096,  -0.0339, 0.1312 ] |     | [0.0495, -0.0392,0.2054 ]  |
|Ġin        |  | [-0.0337, 0.0108,  0.0293 ,...] |     | [0.0027,  -0.0205, 0.1196 ] |     | [-0.031, -0.0098,0.149  ]  |
|Ġsummer    |  | [0.0422,  0.0138,  -0.0213,...] |     | [0.0025,  -0.0032, 0.1174 ] |     | [0.0448, 0.0106, 0.0961 ]  |
|.          |  | [0.0466,  -0.0113, 0.0283 ,...] |     | [-0.0012, -0.0018, 0.111  ] |     | [0.0454, -0.0131,0.1394 ]  |
|ĠSw        |  | [0.0617,  0.0373,  0.1018 ,...] |     | [0.0049,  0.0021,  0.1178 ] |     | [0.0666, 0.0395, 0.2196 ]  |
|imming     |  | [-0.1385, -0.1774, -0.0181,...] |     | [0.0016,  0.0062,  0.1004 ] |     | [-0.1369,-0.1711,0.0823 ]  |
|Ġis        |  | [-0.0097, 0.0101,  0.0556 ,...] |     | [-0.0036, 0.0175,  0.1068 ] |     | [-0.0133,0.0275, 0.1623 ]  |
|------------  -----------------------------------     -------------------------------     ------------------------------

9.2 Normalize

即，将每一个token的embedding 进行正规化，将其均值变为0，方差变为1

Token      |   X norm[:3]  (12 x 768)
--------------------------------------------
It         | [ 0.0129, -0.1104, -0.0317,...]
âĢ         | [-0.0530,  0.0588, -0.1290,...]
Ļ          | [-0.0170, -0.0242,  0.1639,...]
s          | [-0.0754, -0.0842,  0.1842,...]
Ġvery      | [-0.0566, -0.0280,  0.0953,...]
Ġhot       | [ 0.0587, -0.0086,  0.1073,...]
Ġin        | [-0.0391,  0.0209,  0.0731,...]
Ġsummer    | [ 0.0532,  0.0397,  0.0181,...]
.          | [ 0.0553,  0.0152,  0.0579,...]
ĠSw        | [ 0.0807,  0.0691,  0.1216,...]
imming     | [-0.1528, -0.1249, -0.0017,...]
Ġis        | [-0.0175,  0.0605,  0.0880,...]

9.3 Attention 层的参数矩阵

$W^Q\,,W^K\,,W^V $

   W^Q [:3]  shape (768 x 64)               W^K [:3]  shape (768 x 64)                                  W^V [:3]  shape (768 x 64)
-------------------------------------    --------------------------------                            --------------------------------
[-0.4738, -0.2614, -0.0978, ...]   |     [ 0.3660,  0.0771,  0.2226, ...]                            [ 0.1421,  0.0329, -0.0667, ...]
[ 0.0874,  0.1473,  0.2387, ...]   |     [-0.4380, -0.1446, -0.4717, ...]                            [ 0.0162, -0.0633, -0.0636, ...]
[ 0.0039,  0.0695,  0.3668, ...]   |     [ 0.1237,  0.0174,  0.1181, ...]                            [ 0.0229, -0.0828,  0.0437, ...]
[ 0.2215, -0.1884, -0.0141, ...]  64     [-0.2247,  0.0148, -0.1859, ...]                            [-0.0106,  0.0070,  0.0565, ...]
[-0.0947,  0.1678, -0.0143, ...]  rows   [-0.2001, -0.1052, -0.1743, ...]                            [ 0.0416,  0.0938, -0.1792, ...]
   ...                             |        ...                                                          ...
[-0.4100, -0.1924, -0.2400, ...]   |     [,0.1567,  0.2664,  0.1851, ...]                            [-0.0341,  0.0034,  0.0203, ...]
-------------------------------------    --------------------------------                            --------------------------------
|<------- columns: 768 ------->|         |<------- columns: 768 ------->|                            |<------- columns: 768 ------->|

9.4 矩阵 Q K V的计算

$Q = XW^Q $

$K = XW^K $

$V = XW^V $

    Q [:3]  shape (12 x 64)                  K [:3]  shape (12 x 64)                                      V [:3]  shape (12 x 64)
-------------------------------------    ---------------------------------                           --------------------------------
[ 0.4207, -0.9178,  0.1760, ...]  |      [ -1.4202,  1.6791,  0.9837, ...]                           [ 0.0452,  0.0628,  0.1463, ...]
[ 0.7757,  0.2485,  0.7349, ...]  |      [ -2.5320,  2.2932,  1.5592, ...]                           [-0.1361,  0.1379,  0.0150, ...]
[ 0.4481,  0.0206, -0.0825, ...]  |      [ -2.2571,  2.7764,  1.8401, ...]                           [ 0.0039, -0.1295, -0.0311, ...]
[ 0.9500,  0.1481,  0.3469, ...] 12      [ -2.4322,  3.1454,  2.0600, ...]                           [-0.0391,  0.0581,  0.0511, ...]
[ 0.4989, -0.4376,  0.1678, ...] rows    [ -3.5428,  2.1485,  2.0414, ...]                           [ 0.0963,  0.3563, -0.1477, ...]
  ...                             |        ...                                                         ...
[ 0.4429, -1.1997,  0.5611, ...]  |      [ -2.2559,  2.0384,  2.2542, ...]                           [ 0.2759, -0.2783,  0.3240, ...]
-------------------------------------    ---------------------------------                           --------------------------------
|<------- columns: 64 ------->|          |<------- columns: 64 ------->|                             |<------- columns: 64 ------->|

9.5 计算 Attention Score

$\text{Attention Score} $

$= \frac{QK^T}{\sqrt{d}} $

|---------------------------------------------------------------------------------------------|
|       |           Attention Score Matrix shape (12 x 12)                                    |
| Token |-------------------------------------------------------------------------------------|
|       |   It     âĢ     Ļ      s     Ġvery  Ġhot    Ġin  Ġsummer  .     ĠSw    imming  Ġis  |
|-------|-------------------------------------------------------------------------------------|----
|It     | [ 0.14, -1.53, -1.45, -1.71, -1.69, -1.74, -2.36, -2.27, -2.37, -1.33, -0.58, -2.40]|  |
|âĢ     | [ 0.70, -0.93, -1.72, -1.02, -1.52, -2.24, -1.90, -2.19, -1.63, -2.13, -1.66, -2.14]|  |
|Ļ      | [-0.60, -1.81, -1.99, -1.96, -2.57, -1.84, -1.62, -2.04, -0.98, -1.18, -2.23, -2.25]|  |
|s      | [-0.46, -1.33, -1.60, -2.65, -2.24, -1.99, -2.89, -1.44, -2.05, -2.77, -2.09, -2.74]|  |
|Ġvery  | [ 0.29, -1.42, -1.77, -1.15, -0.94, -1.14, -1.81, -1.04, -1.77, -2.13, -0.60, -0.82]|  |
|Ġhot   | [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10, -0.95, -0.14, -1.32, -0.57,  0.06, -1.07]|  12
|Ġin    | [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41, -1.69, -2.74, -1.89, -1.17, -2.02]|  rows
|Ġsummer| [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11, -1.51, -1.15, -1.45, -1.20]|  |
|.      | [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42, -2.73, -1.82, -3.21]|  |
|ĠSw    | [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29, -0.43, -1.51]|  |
|imming | [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15, -1.08]|  |
|Ġis    | [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99]|  |
|-------|-------------------------------------------------------------------------------------|----
        |<-------------------------------- columns: 12 -------------------------------------->|

9.6 计算 Masked Attention Score

$\text{Masked Attention Score} $

$= \frac{QK^T}{\sqrt{d}} + \text{mask} $

|---------------------------------------------------------------------------------------------|
|       |   Masked  Attention Score Matrix shape (12 x 12)                                    |
| Token |-------------------------------------------------------------------------------------|
|       |   It     âĢ     Ļ      s     Ġvery  Ġhot    Ġin  Ġsummer  .     ĠSw    imming  Ġis  |
|-------|-------------------------------------------------------------------------------------|----
|It     | [ 0.14,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]|  |
|âĢ     | [ 0.70, -0.93,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]|  |
|Ļ      | [-0.60, -1.81, -1.99,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]|  |
|s      | [-0.46, -1.33, -1.60, -2.65,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]|  |
|Ġvery  | [ 0.29, -1.42, -1.77, -1.15, -0.94,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]|  |
|Ġhot   | [ 0.03, -0.68, -0.59, -0.95, -1.78, -0.10,  -inf,  -inf,  -inf,  -inf,  -inf,  -inf]|  12
|Ġin    | [-0.71, -1.72, -1.53, -2.18, -1.67, -1.93, -3.41,  -inf,  -inf,  -inf,  -inf,  -inf]|  rows
|Ġsummer| [-0.34, -1.49, -1.35, -1.31, -1.12, -0.89, -1.49, -1.11,  -inf,  -inf,  -inf,  -inf]|  |
|.      | [-0.89, -1.73, -2.67, -2.80, -2.45, -2.37, -4.39, -2.33, -4.42,  -inf,  -inf,  -inf]|  |
|ĠSw    | [-0.05, -1.15, -1.76, -1.15, -1.68, -0.74, -1.15, -1.35, -1.36, -1.29,  -inf,  -inf]|  |
|imming | [-0.02, -1.65, -0.87, -0.35, -1.18, -0.65, -0.33, -1.25, -0.38, -1.68, -2.15,  -inf]|  |
|Ġis    | [-0.97, -2.03, -2.56, -2.94, -1.96, -2.71, -4.07, -2.46, -3.51, -2.68, -1.88, -2.99]|  |
|-------|-------------------------------------------------------------------------------------|----
        |<-------------------------------- columns: 12 -------------------------------------->|

9.7 计算 Softmax Masked Attention Score

$\text{Softmax Masked Attention Score} $

$= \text{softmax}(\frac{QK^T}{\sqrt{d}} + \text{mask}) $

|-------------------------------------------------------------------------------------|
|       |  Softmax Masked  Attention Score Matrix shape (12 x 12)                     |
| Token |-----------------------------------------------------------------------------|
|       |  It    âĢ    Ļ     s     Ġvery  Ġhot  Ġin  Ġsummer  .   ĠSw   imming  Ġis   |
|-------|-----------------------------------------------------------------------------|
|It     | [1.00  0.00  0.00  0.00   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]|  |
|âĢ     | [0.84  0.16  0.00  0.00   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]|  |                  V [:3]  shape (12 x 64)
|Ļ      | [0.65  0.19  0.16  0.00   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]|  |              --------------------------------
|s      | [0.54  0.23  0.17  0.06   0.00  0.00  0.00  0.00  0.00  0.00  0.00  0.00]|  |              [ 0.0452,  0.0628,  0.1463, ...]
|Ġvery  | [0.54  0.10  0.07  0.13   0.16  0.00  0.00  0.00  0.00  0.00  0.00  0.00]|  |              [-0.1361,  0.1379,  0.0150, ...]
|Ġhot   | [0.29  0.14  0.16  0.11   0.05  0.25  0.00  0.00  0.00  0.00  0.00  0.00]|  12             [ 0.0039, -0.1295, -0.0311, ...]
|Ġin    | [0.36  0.13  0.16  0.08   0.14  0.11  0.02  0.00  0.00  0.00  0.00  0.00]|  rows           [-0.0391,  0.0581,  0.0511, ...]
|Ġsummer| [0.26  0.08  0.09  0.10   0.12  0.15  0.08  0.12  0.00  0.00  0.00  0.00]|  |              [ 0.0963,  0.3563, -0.1477, ...]
|.      | [0.40  0.17  0.07  0.06   0.08  0.09  0.01  0.10  0.01  0.00  0.00  0.00]|  |                ...
|ĠSw    | [0.27  0.09  0.05  0.09   0.05  0.14  0.09  0.07  0.07  0.08  0.00  0.00]|  |              [ 0.2759, -0.2783,  0.3240, ...]
|imming | [0.19  0.04  0.08  0.14   0.06  0.10  0.14  0.06  0.13  0.04  0.02  0.00]|  |              --------------------------------
|Ġis    | [0.30  0.10  0.06  0.04   0.11  0.05  0.01  0.07  0.02  0.05  0.12  0.04]|  |              |<------- columns: 64 ------->|
|-------|-----------------------------------------------------------------------------|
        |<-------------------------------- columns: 12 ------------------------------>|

9.8 计算 Contextual Embeddings

$\text{Contextual Embeddings} $

$= \text{softmax}(\frac{QK^T}{\sqrt{d}} + \text{mask})V $

Token      | Contextual Embedding (12 x 768)
--------------------------------------------
It         | [ 0.0452,  0.0628,  0.1463,...]
âĢ         | [ 0.0153,  0.0752,  0.1247,...]
Ļ          | [ 0.0034,  0.0464,  0.0923,...]
s          | [-0.0082,  0.0464,  0.0801,...]
Ġvery      | [ 0.0218,  0.1029,  0.0621,...]
Ġhot       | [ 0.0327,  0.0892,  0.0409,...]
Ġin        | [ 0.0249,  0.0964,  0.0329,...]
Ġsummer    | [ 0.0583,  0.1195,  0.0068,...]
.          | [ 0.0334,  0.1100,  0.0366,...]
ĠSw        | [ 0.0086,  0.0846,  0.0074,...]
imming     | [-0.0049,  0.0841, -0.0339,...]
Ġis        | [ 0.0410,  0.0706,  0.0077,...]

10. 其他

上述流程详述了 LLM 模型中 Attention 计算的核心部分。也有一些细节是省略了的，例如，

在GPT2中，“线性变换”是有一个“截距”(Bias)的，所以也可以称为一个“仿射变换”，即在一个线性变换基础上，再进行一次平移；
在GTP2中，Attention计算都是多层、多头的，本文主要以Layer 0 / Head 0 为例进行介绍；
在生成最终的“Contextual Embeddings”之前，通常还需要一个MLP层（全连接的前馈神经网络）等，本文为了连贯性，忽略了该部分。

总结一下，本文需要的前置知识包括：矩阵基本运算、矩阵与线性变换、SVD 分解/特征值特征向量、神经网络基础、深度学习基础等。

注

[1] 多头注意情况可能是 $d \times \frac{d}{h} $
[2] 对于满秩方阵也可以使用“特征值/特征向量”的方式去理解
[3] 在 GPT 2 中，一个 Attention 层的计算，会分为“多头”去计算；并在计算后，还会再经过一个 MLP 层

大语言模型的输入：tokenize

2025-12-27

admin

对于非 NLP 专业的人来说，要向理解大语言模型的基础其实是非常不容易的。在有了一定的神经网络基础、数学基础之后，算是可以更进一步了，在了解LLM的系列中，大概可以分成几个部分：输入（即本文的tokenize）、计算（Attention）、输出（beam search/top-k）。在本篇中：(a) 通过代码实践观察大模型（GPT2）如何进行 tokenize；(b) 如何查看 token id 列表 (c) 观察模型中所有token的 Embedding Matrix。

这是我的大语言（LLM）学习系列中的一篇，完整的学习路径参考：我的大模型学习路线。

1. 理解 tokenize
2. Token Embedding
3. Positional encoding
示例与代码
Embedding Matrix
- 查看 Embedding Matrix
最后

1. 理解 tokenize

1.1 Token ID

这里我们使用如下的提示词，来看看大模型是如何处理的：It’s very hot in summer. Swimming is 。

大模型会使用预先设计好的“tokenize”实现，将上述的句子分解成独立的“Token”，并转换为对应的“Token ID”，而每个Token，都有自己的编码，也就是 Embedding ，这些 Embedding 就最终作为大语言模型的输入。

对于上述的句子，“openai-community/gpt2” 在进行 tokenize 之后对应的 Token 和 Token ID 如下：

’

very

hot

summer

Swimming

Token ID

1026

447

247

845

3024

287

3931

2451

27428

318

Token

âĢ

Ġvery

Ġhot

Ġin

Ġsummer

ĠSw

imming

Ġis

“openai-community/gpt2” 使用了较为常见的BPE（Byte Pair Encoding）对句子进行处理，把每个词语按照“subword”进行处理，例如：

“Swimming”拆分为“Sw”与“imming”
这里两个 Token 447、247 组成特殊字符 ‘ (撇号)
Ġ（U+0120）的作用：表示这是一个新的词语（而不是一个拆分后子词），可以看到 “Swimming”在拆分后的“imming”前面并没有Ġ，表示这是一个拆分后的子词

1.2 词表大小

“openai-community/gpt2” 模型的词表大小为：50257。词表中的前三个 Token 为 ’emb’、 ‘ĠDraft’、 ‘Ġreinvent’，对应的 Token ID 为 24419、 13650、 36608。

1.3 根据 Token ID 打印字符

这里打印了 Token ID 为 0、 1、 2 和 50254、 50255、 50256 的几个字符如下：

Token ID	Char
0	!
1	“
2	#
50254	Ġinformants
50255	Ġgazed
50256	<\|endoftext\|>

--- Token ID 转换为 Token 字符 ---
Token ID: 0     | 对应 Token 字符: '!'
Token ID: 1     | 对应 Token 字符: '"'
Token ID: 2     | 对应 Token 字符: '#'
Token ID: 50254 | 对应 Token 字符: 'Ġinformants'
Token ID: 50255 | 对应 Token 字符: 'Ġgazed'
Token ID: 50256 | 对应 Token 字符: '<|endoftext|>'

2. Token Embedding

在大模型的通常是从 Embedding 开始的，即对于所有字符的处理，都是依赖字符对应的“向量”。所以，大致的处理逻辑是这样：一个句子，先切分为 Token，然后根据 Token ID 在“Embedding Matrix”中找到对应的“向量”，把该“向量”组作为输入。

这里，我们观察上述示例句子，根据对应的 Token ID 可以查询到对应的向量。因为这里的向量是768维的，这里仅显示前三个维度的分量，如下：

Token      | wte[:3]                         |
----------------------------------------------
It         | [0.039,   -0.0869, 0.0662 ,...] |
âĢ         | [-0.075,  0.0948,  -0.0034,...] |
Ļ          | [-0.0223, 0.0182,  0.2631 ,...] |
s          | [-0.064,  -0.0469, 0.2061 ,...] |
Ġvery      | [-0.0553, -0.0348, 0.0606 ,...] |
Ġhot       | [0.0399,  -0.0053, 0.0742 ,...] |
Ġin        | [-0.0337, 0.0108,  0.0293 ,...] |
Ġsummer    | [0.0422,  0.0138,  -0.0213,...] |
.          | [0.0466,  -0.0113, 0.0283 ,...] |
ĠSw        | [0.0617,  0.0373,  0.1018 ,...] |
imming     | [-0.1385, -0.1774, -0.0181,...] |
Ġis        | [-0.0097, 0.0101,  0.0556 ,...] |

更为完整的，上述的每个词语对应的向量是一个 1×768 的向量；整个句子 12 个向量，可以理解为一个 12×768 的输入矩阵。对于各 LLM 来说，这通常就是其将要处理的输入。

3. Positional encoding

在“GPT-2”使用了“Learned Positional Embeddings”（注：与 Transformer 论文中固定的Sinusoidal 实现不同）。这是一个 $L \times d $ 的矩阵，其中，$L $ 是最大接收字符数，$d $ 是 Token Embedding 的维度。该矩阵通常随机初始化，最终通过训练确定。在“GPT-2”中，最终训练后的矩阵有如下形式：

pos_emb_layer = model.transformer.wpe

# .weight.data : Embedding Matrix(PyTorch Tensor)
pos_emb_matrix = pos_emb_layer.weight.data

print(pos_emb_matrix[:12,:3])

输入如下：

tensor([[-0.0188, -0.1974,  0.0040],
        [ 0.0240, -0.0538, -0.0949],
        [ 0.0042, -0.0848,  0.0545],
        [-0.0003, -0.0738,  0.1055],
        [ 0.0076, -0.0251,  0.1270],
        [ 0.0096, -0.0339,  0.1312],
        [ 0.0027, -0.0205,  0.1196],
        [ 0.0025, -0.0032,  0.1174],
        [-0.0012, -0.0018,  0.1110],
        [ 0.0049,  0.0021,  0.1178],
        [ 0.0016,  0.0062,  0.1004],
        [-0.0036,  0.0175,  0.1068]])

示例与代码

环境准备

这里依旧使用 🤗 HuggingFace 的 Transformers 库以及 Google 的 Colab 作为环境，硬件为 T4 GPU。这里新建的 Colab 文件链接： AutoTokenizer.ipynb
这里使用的测试模型是“openai-community/gpt2”，该模型是由 OpenAI 在 2019 对外发布的。

!pip install transformers torch

from transformers import AutoTokenizer, AutoModelForCausalLM

MODEL_NAME = "openai-community/gpt2"
tokenizer = AutoTokenizer.from_pretrained(MODEL_NAME)
model = AutoModelForCausalLM.from_pretrained(MODEL_NAME)

对句子进行 tokenize

观察句子的tokenize：

text = "It’s very hot in summer. Swimming is"

# 1. 对句子进行 Tokenization
# return_tensors='pt' 表示返回 PyTorch Tensor 格式 (虽然这里我们主要看 IDs)
inputs = tokenizer(text, return_tensors='pt')

# 2. 打印 Tokenization 结果
print(f"--- 原始句子：{text} ---")

# a. 打印 Token ID Tensor
print("Token IDs (Tensor):")
print(inputs['input_ids'])

# b. 将 Token ID 转换回可读的 Token (Word Pieces)
# .squeeze() 是为了去除 batch 维度
tokens = tokenizer.convert_ids_to_tokens(inputs['input_ids'].squeeze().tolist())
print("\nToken List (可读文本 Tokens):")
print(tokens)

# c. 打印 Attention Mask (1 表示是有效 Token，0 表示是 Padding Token)
print("\nAttention Mask:")
print(inputs['attention_mask'])

--------------
--- output ---
--------------

--- 原始句子：It’s very hot in summer. Swimming is ---
Token IDs (Tensor):
tensor([[ 1026,   447,   247,    82,   845,  3024,   287,  3931,    13,  2451,
         27428,   318]])

Token List (可读文本 Tokens):
['It', 'âĢ', 'Ļ', 's', 'Ġvery', 'Ġhot', 'Ġin', 'Ġsummer', '.', 'ĠSw', 'imming', 'Ġis']

Attention Mask:
tensor([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]])

词表大小查看

查看词表大小，并打印词表中的前20个词：

# 获取词汇表大小
vocab_size = tokenizer.vocab_size
print(f"--- GPT-2 模型支持的 Tokenize 总数 (词汇表大小): {vocab_size} ---")

# 打印所有 Tokenize
# tokenizer.get_vocab() 返回的是一个字典 {token: id}
print("\n--- 打印前 20 个 Token (用于示例): ---")
vocab = tokenizer.get_vocab()
count = 0
for token, id in vocab.items():
    if count < 20:
        # 使用 repr() 确保特殊字符（如空格 'Ġ'）能被清晰展示
        print(f"ID: {id:<5} | Token: {repr(token)}")
        count += 1
    else:
        break

--------------
--- output ---
--------------

--- GPT-2 模型支持的 Tokenize 总数 (词汇表大小): 50257 ---

--- 打印前 20 个 Token (用于示例): ---
ID: 24419 | Token: 'emb'
ID: 13650 | Token: 'ĠDraft'
ID: 36608 | Token: 'Ġreinvent'
ID: 36171 | Token: 'Recommended'
ID: 20706 | Token: 'aunting'
ID: 39558 | Token: 'Ġprotagonists'
ID: 49309 | Token: 'raised'
ID: 20589 | Token: 'Ġwicked'
ID: 43074 | Token: 'ĠâĿ'
ID: 22792 | Token: 'ĠTut'
ID: 21620 | Token: 'erate'
...

根据 Token ID 打印字符

# 待查询的 Token ID 列表
target_ids = [0, 1, 2, 50254 ,50255, 50256]

tokens = tokenizer.convert_ids_to_tokens(target_ids)

print(f"--- Token ID 转换为 Token 字符 ---")
for id, token in zip(target_ids, tokens):
    # 使用 repr() 确保任何特殊的不可见字符（如空格或控制字符）能被清晰地展示
    print(f"Token ID: {id:<5} | 对应 Token 字符: {repr(token)}")

# 额外打印这几个 Token 在词汇表中的 ID，以确认其对应关系
# 这里的 token.id 并不是直接从 1, 2, 3 来的，而是从 tokenizer.get_vocab() 中查到的
# 这是一个辅助验证步骤，确保 Tokenizer 的行为符合预期。
print("\n--- 辅助验证 ---")
for token in tokens:
    token_id_check = tokenizer.convert_tokens_to_ids(token)
    print(f"Token 字符: {repr(token):<10} | 查验 ID: {token_id_check}")

--------------
--- output ---
--------------

--- Token ID 转换为 Token 字符 ---
Token ID: 0     | 对应 Token 字符: '!'
Token ID: 1     | 对应 Token 字符: '"'
Token ID: 2     | 对应 Token 字符: '#'
Token ID: 50254 | 对应 Token 字符: 'Ġinformants'
Token ID: 50255 | 对应 Token 字符: 'Ġgazed'
Token ID: 50256 | 对应 Token 字符: '<|endoftext|>'

根据 Token ID 查询对应向量

在模型中，“词向量”（准确的应该是Token向量）存储在一个Embedding Matrix 中，可以使用如下的代码获取每个 token 对应 Embedding 后的向量：

target_token = "ĠSw"  # 注意前面的特殊符号，确保它是模型词汇表中的 Token
target_id = tokenizer.convert_tokens_to_ids(target_token)
print(target_id)

# embedding_matrix[target_id]
target_embedding = embedding_matrix[target_id]
print(target_embedding[:5].numpy())

--------------
--- output ---
--------------

2451
[ 0.06167513  0.03733223  0.10182938  0.04881619 -0.09597597]
Embedding 层的 dtype: torch.float32
整个模型的默认 dtype: torch.float32

句子到 Embedding 向量

text = "It’s very hot in summer. Swimming is"
inputs = tokenizer(text, return_tensors='pt')
print("Token IDs (Tensor):")
input_ids_tensor = inputs['input_ids']
input_ids_list = input_ids_tensor.squeeze().tolist()

for index, token_int in enumerate(input_ids_list):
    token_char = tokenizer.convert_ids_to_tokens(token_int)
    print(f"Token ID {token_int:<5} | Token: {repr(token_char):<9} | {embedding_matrix[token_int][:3]}")

--------------
--- output ---
--------------

Token ID 1026  | Token: 'It'      | tensor([ 0.0390, -0.0869,  0.0662])
Token ID 447   | Token: 'âĢ'      | tensor([-0.0750,  0.0948, -0.0034])
Token ID 247   | Token: 'Ļ'       | tensor([-0.0223,  0.0182,  0.2631])
Token ID 82    | Token: 's'       | tensor([-0.0640, -0.0469,  0.2061])
Token ID 845   | Token: 'Ġvery'   | tensor([-0.0553, -0.0348,  0.0606])
Token ID 3024  | Token: 'Ġhot'    | tensor([ 0.0399, -0.0053,  0.0742])
Token ID 287   | Token: 'Ġin'     | tensor([-0.0337,  0.0108,  0.0293])
Token ID 3931  | Token: 'Ġsummer' | tensor([ 0.0422,  0.0138, -0.0213])
Token ID 13    | Token: '.'       | tensor([ 0.0466, -0.0113,  0.0283])
Token ID 2451  | Token: 'ĠSw'     | tensor([0.0617, 0.0373, 0.1018])
Token ID 27428 | Token: 'imming'  | tensor([-0.1385, -0.1774, -0.0181])
Token ID 318   | Token: 'Ġis'     | tensor([-0.0097,  0.0101,  0.0556])

Embedding Matrix

查看 Embedding Matrix

# model.transformer.wte (Word Token Embeddings)
embedding_layer = model.transformer.wte

# .weight.data : Embedding Matrix(PyTorch Tensor)
embedding_matrix = embedding_layer.weight.data

print(embedding_matrix.shape)

--------------
--- output ---
--------------

torch.Size([50257, 768])

最后

大模型训练的第一步就是对于语料库（corpus）的处理，即将所有的语料转换为大模型训练能够接受的输入，即：tokenize。该过程会将语料库切分为独立的句子，多个句子可以作为一个批次（batch）作为输入进行训练。

Gartner 2025 云数据库魔力象限概要解读

2025-12-20

·

admin
整体上，今年的魔力象限与去年的厂商完全相同，各厂商的相对位置变化也并不是很大。一些值得注意的点如下：

Redis 从 Visionaries 跌到 Niche Player 象限；这反应了 Redis 在社区所面临的困境，一方面是开源商业化的挑战；另一方，则是来自于 Valkey 社区–一个更加开放的 Key-Value 产品的竞争。

Neo4j 也从 Visionaries 跌到 Niche Player 象限。

在第一军团（即Google AWS Microsoft Oracle）中，Oracle 位置略有下降。确实，Oracle 早就已经不再是一家数据库厂商了。

Databricks 和 Snowflake 凭借在数据处理上的领先，在横坐标（Visionaries）上前进了一大截

此外，虽然没有在象限图中（仅前20的厂商），但依旧在Gartner关注对象中的厂商包括：Actian Broadcom ClickHouse InfluxData MotherDuck OceanBase PingCAP Tencent Cloud TigerGraph Yugabyte

象限中的中国数据库厂商

进入这次魔力象限的中国厂商与去年相同：阿里云数据库、华为云数据库。相比去年，两个厂商的位置变化也不太大，可以参考右图。

阿里云数据库在 Vision 象限继续向前移动了一点。华为云则保持了相对位置几乎不变。

此外，出现在“Honorable Mentions”部分的中国厂商有：

OceanBase

PingCAP

Tencent Cloud

历史魔力象限列表

2025-11

2024

2023

2022

2021

2020

2019

2018

2017

2016

2015

2014

2013

其他

作者最近几年持续对 Gartner 云数据库魔力象限保持关注，历史相关文章包括：

2024 Gartner 数据库魔力象限概要解读

Gartner 2023数据库魔力象限发布阿里云数据库连续为领导者

数据库魔力象限2022：阿里领先、腾讯再次进入、华为退出

2021 Gartner云数据库魔力象限正式发布

Gartner云计算魔力象限@2018
问答 Agent 构建过程实践与经验

2025-10-12

·

admin

LLM 强大的语言、知识与推理能力在改变很多领域，也将持续、深入的改变更多领域。在软件领域，“Agent” 的编程模型已经是一种新的编程模式，通过这种“模式”可以将 LLM 的能力，软件提供商的领域知识，以及外部工具的能力很好的结合起来，形成“新的”软件产品。
(more…)
奇异值分解–深度学习的数学基础

2025-09-21

·

admin
在 $\text{Attention} $ 机制（或 $ \text{Multi-Head Attention} $ ）中我们会看到这样的变换：$ \text{Attention} = softmax(\frac{Q_iK_i^{T}}{\sqrt{d}}) $，其中这里 $ Q_i = XW_i^Q $ 那么如何理解这里的 $ XW_i^Q $ 呢？该变换是向量空间内一个典型的线性变换，而这里的 $ W_i^Q $ 就是对应的线性变换矩阵，在早期 GPT 模型中该矩阵是一个$ 768 \times 64$ 的矩阵，研究该矩阵的典型方法就可以使用 $ \text{SVD} $ 分解，本文展示了简单的二维空间中 $ \text{SVD} $ 分解以及对应的几何意义，从而可以较好的帮助理解上述计算的深层次含义。

关于奇异值分解（$ \text{SVD} $）能够解决的问题这里不再详述。本文通过展示对于平面空间中的线性变换进行奇异值分解，从而观察该分解如何通过“几何”的方式描述一个线性变换，从而建立对线性变换的直观理解。本文的示例是一个$ 2 \times 2$的矩阵，所以还补充了对该矩阵的特征值/特征向量的计算，从而对比这两种方法在处理“方阵”时的异同。

目录
1. 概述
2. 奇异值分解
2.1 矩阵A的两种 SVD 分解
2.2 分解1的几何意义与图示
2.3 分解2的几何意义与图示
3. 特征值与特征向量
4. 小结
5. 补充说明
附录1 二维空间的正交变换
附录2 三维空间的正交变换

1. 概述

本文通过对二维空间中的一个线性变换（满秩方阵） $ A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} $ 进行 $ \text{SVD} $ 分析、特征值/特征向量分析，从而建立在平面空间中对于线性变换的直觉理解，更进一步的理解$ \text{SVD} $和特征值/特征向量分别是如何描述一个线性变换的。具体的，这里观察了在该线性变换的作用下，一个点 $ (1,0) $ 是如何在两种矩阵变换下，映射到目标点的。

2. 奇异值分解

2.1 矩阵A的两种 SVD 分解

奇异值分解并不是唯一的。从几何的角度理解，一个二维空间的线性变换，是由旋转、反射、缩放组成，而先旋转、或先反射都是可以的，而这对应的就是不同的奇异值分解。考虑上述的矩阵 $ A = \begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} $ 进行 $ \text{SVD} $，我们有如下两种分解（关于具体的分解方法，本文并不详述）。

第一种分解：

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = UΣV^T =\begin{bmatrix}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
$$

第二种分解如下：

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = UΣV^T =\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix} $$

2.2 分解1的几何意义与图示

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = U\Sigma V^T = \begin{bmatrix}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
$$

考虑：

$ V^T = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & \sin\varphi \\ \sin\varphi & -\cos \varphi \end{bmatrix} $ 相同，故，此为关于直线 $ y = (\tan\frac{\varphi}{2})x $ 的反射^[附录1]。

$ \Sigma = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} $ 表示将点、向量的坐标进行缩放。

$ U = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & -\sin\varphi \\ \sin\varphi & \cos \varphi \end{bmatrix} $ 相同，故，此为一个逆时针 $ \varphi $ 度的旋转^[附录1]。

即，上述的线性变换可以做这样的理解：

先将点以$ y=\tan\frac{45}{2}x = (\sqrt{2}-1)x $为轴进行反射

然后将坐标第一个分量放大3倍

最后再逆时针旋转$ 45^{\circ} $

考虑坐标上的点$ \alpha = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $，我们看看如何经过该线性变换，映射到目标点：

右图反映了完整的过程：

$ (1,0) $ 先经过按图中虚线为轴进行反射，到红点

然后，进行拉伸，第一个分量拉伸3倍，到绿色点

最后，再逆时针旋转$ 45^{\circ} $ 到黄色点

对应的矩阵计算如下：

$ \text{red} = V^T \alpha = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}\end{bmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} $

$ \text{green} = \Sigma V^T \alpha = \Sigma \, \text{red} = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} \frac{3}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} $

$ \text{yellow} = U\Sigma V^T \alpha = U \, \text{green} = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{pmatrix} \frac{3}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $

2.3 分解2的几何意义与图示

$$ A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} = UΣV^T =\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{bmatrix}\begin{bmatrix}
3 & 0 \\
0 & 1
\end{bmatrix}\begin{bmatrix}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix} $$

考虑：

$ V^T = \begin{bmatrix}-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & -\sin\varphi \\ \sin\varphi & \cos \varphi \end{bmatrix} $相同，故，此为一个逆时针 $ \varphi = 135^{\circ} $ 度的旋转^[附录1]。

$ \Sigma = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} $ 表示将点、向量的坐标进行缩放。

$ U = \begin{bmatrix} -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} $ 形式与 $ \begin{bmatrix} \cos \varphi & \sin\varphi \\ \sin\varphi & -\cos \varphi \end{bmatrix} $ 相同，故，此为关于直线 $ y = (\tan\frac{\varphi}{2})x $ 的反射^[附录1]。

即，上述的线性变换可以做这样的理解：

点$ (1,0) $ 先逆时针旋转$ \varphi = 135^{\circ} $到达红色点

然后将坐标第一个分量放大3倍，成为绿色点

最后将点以$ y=\tan\frac{-135^{\circ}}{2}x $为轴进行反射，到黄色点

具体可以参考右图，详细的计算这里不再给出。

3. 特征值与特征向量

因为这里的$ A $是一个 $ 2 \times 2 $ 的方阵，故可以使用特征值与特征向量来洞察这个线性变换的本质。

对于该矩阵的特征值、对应的特征向量计算结果如下：

对于特征值 $ \lambda_1 = 3 $ 时，特征向量为 $ (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) $

对于特征值 $ \lambda_2 = -1 $ 时，特征向量为 $ (\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) $

依旧，这里我们来考虑向量 $ \alpha = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $ 在这两个特征向量方向上作用后的效果。

右图已经比较直观的反应了如何从特征向量和特征值的角度去理解线性变换：

首先，先将向量 $ \alpha $ 在两个特征向量上进行分解，分解后的向量分别为 $ \alpha_1 \, \alpha_2 $

然后再按照特征值进行缩放：

$ \lambda_1 = 3 $ 故将 $ \alpha_1$拉伸为 $ \beta_1 $

$ \lambda_2 = -1 $ 故将 $ \alpha_2$反向为 $ \beta_2 $

最后，$ \beta_1 $ 和 $ \beta_2 $ 合并为 $ \beta $

4. 小结

在这种情况下（注：线性变换矩阵为一个 $ 2 \times 2 $的满秩矩阵），我们可以使用奇异值分解$ \text{SVD} $、特征值计算的方式来洞察这个线性变换的“本质”。两种方法各有一些优缺点，大家可以自己去体会，这里小结一下我的理解。

奇异值分解$ \text{SVD} $是一种“动态”的展示线性变换的方法，可以让你很清晰的了解这个线性变换是如何将空间中的“一个点”映射到“另一个点”的。例如在上述的例子中，则是先进行旋转、然后进行缩放、最后进行反射。

特征值/特征向量计算则是对线性变换的“静态”解释，使用静态的方式展现了线性变换如何将“一个点”映射到“另一个点”的。

5. 补充说明

实际应用中的奇异值分解通常是用于处理更高维的向量空间，所以通常没有这么直观的几何意义，但是依旧可以使用类比的“反射”、“旋转”、“拉伸/压缩”等概念去扩展的理解。

特征值/特征向量仅适用于处理方阵的场景，所以场景比较受限。

关于特特征值/特征向量计算，在实际中可能会更加复杂，例如，重根、复数根等情况，要想进一步理解，则需要做更深入的研究。

要进一步加深理解，则可以考虑，观察一个三维空间中变换的实例，有一些相同，也有一些不同：

反射，通常是基于某个平面（两个基张成的平面）的

选择，则是绕着某个直线（某个向量的方向上）

附录1 二维空间的正交变换

二维空间中，有两种正交变换，即旋转或反射。其对应的线性变换矩阵分别有如下的形式：$ \begin{bmatrix} \cos \varphi & \sin\varphi \\ \sin\varphi & -\cos \varphi \end{bmatrix} $ 与 $ \begin{bmatrix} \cos \varphi & -\sin\varphi \\ \sin\varphi & \cos \varphi \end{bmatrix} $ 。

附录2 三维空间的正交变换

在三维空间内，对于一组规范正交基 $ \{ \alpha_1,\alpha_2,\alpha_3 \} $ ，该空间下的正交变换矩阵总有如下形式：

$$
\begin{bmatrix}
\pm 1 & 0 & 0 \\
0 & a & b \\
0 & c & c
\end{bmatrix}
$$

更为具体的为如下三种形态之一：

$$
A = \begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\varphi & -\sin\varphi \\
0 & \sin\varphi & \cos\varphi
\end{bmatrix}
\quad
B = \begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\\
\begin{aligned}
C & = \begin{bmatrix}
-1 & 0 & 0 \\
0 & \cos\varphi & -\sin\varphi \\
0 & \sin\varphi & \cos\varphi
\end{bmatrix} \\
& =
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\varphi & -\sin\varphi \\
0 & \sin\varphi & \cos\varphi
\end{bmatrix}
\begin{bmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\end{aligned}
$$

这里的：

变换 $ A $ 为一个旋转，旋转轴为 $ \alpha_1 $ 所在的直线

变换 $ B $ 是一个反射，反射轴平面为 $ \mathscr{L}(\alpha_2,\alpha_3) $

变换 $ C $ 是上述两个变换的组合
Word Embedding 的可解释性探索

2025-08-31

·

admin
这大概是一个有趣、也略深刻的发现。

Word Embedding是比较抽象的，但是这些抽象背后是一些“具象”的含义的，本文通过一些简单的计算（变换）来将Embedding的某些维度/属性具象化。具体的，本文展示了在Embedding空间中，找到一个代表“动物”属性的方向。感兴趣的话，可以通过这个简单的方法，找到你感兴趣的属性方向。

目录
TL;DR
概述
寻找某个关心的方向
列出最具代表性的词语
计算Embedding的平均方向
验证该方向
计算投影并可视化
原理解释
概述
数学推导
投影计算
向量的平均方向与主成分方向
更深层次的理解
补充说明

TL;DR

通常，在某个具体的Word Embedding实现中，先给出一组具有“共同属性”的词语，然后计算这组词语Embedding向量的平均方向，就可以代表这个“共同属性”。

例如，找到一组“动物”，然后对这些词语的Embedding向量计算平均方向，那么这个方向就是“动物”这个属性的方向。

概述

如果你也尝试过去理解 Embedding 各个维度的含义的话，大概都听过这样一种说法：Embedding每个维度可以理解为这个词语的某种属性，例如，“性别属性”、“皇室相关度”等，这是最为经典的man - woman = king - queue的例子中的一些解释。

当你真的拿到一个词语的 Embedding 的时候，它可能有768维，但是，似乎没有一个维度有上述的清晰的属性含义。而实际上，这些属性含义是确实存在的，只是这些属性方向并不存在于“标准基”的方向上。

那如果存在，我们应该如何找到这个方向呢？本文展示并验证了一个非常简单的方法，让你快速找到某种属性的方向，并且进行一些验证。从而可以大大加深对于 Embedding 的理解。

寻找某个关心的方向

这里展示了以寻找“动物”属性方向为例，展示如何寻找并验证该方向。

列出最具代表性的词语

我们这样考虑这个问题，如果有一个方向表示一个词语的“动物”属性，那么这个方向会是哪个方向？这里以all-MiniLM-L6-v2模型提供的Sentence Embedding为例，我看看如何找到该Embedding所处的向量空间中最可能代表“动物”属性的方向是哪个？具体的方法描述如下：

首先，找到被认为最典型的与“动物”属性相关的词语$ n $个，这里取$ n=50 $

然后计算上述$ n $个词语的平均方向 avg_vector，该方向则认为要寻找的方向

这里，给出的50个动物如下：

animals = [ "tiger", "lion", "elephant", "giraffe", "zebra", "rhinoceros", "hippopotamus","crocodile", "monkey", "panda", "koala", "kangaroo","whale", "dolphin", "seal", "penguin", "shark", "snake", "lizard", "turtle", "frog", "butterfly", "bee", "ant", "eagle", "sparrow", "pigeon", "parrot", "owl", "duck", "chicken", "dog", "cat", "pig", "cow", "sheep", "horse", "donkey", "rabbit", "squirrel", "fox", "wolf", "bear", "deer", "hedgehog", "bat", "mouse", "chameleon", "snail", "jellyfish" ]

计算Embedding的平均方向

该平均方向，即为我们要寻找的“动物”属性方向。

animals_embeddings = model.encode(animals) avg_animals_embeddings = np.mean(animals_embeddings, axis=0)

验证该方向

再选取两组词，一组认为是与“动物”非常相关的词，另一组则是与动物无关的词语。然后分别计算这两组词语在上述方向avg_vector的投影值。观察投影值，是否符合预期。

这里选择的两组词语分别是：

与动物非常相关的：”Camel”, “Gorilla”, “Cheetah”

与动物无关的：”Dream”, “Chair”, “Mathematics”

计算投影并可视化

具体的程序如下：

animals_words = ["Camel", "Gorilla", "Cheetah"] un_animals_words = ["Dream", "Chair", "Mathematics"] for word_list in (animals_words,un_animals_words): projection_scores = np.dot(model.encode(word_list), avg_animals_embeddings) results.update({word: score for word, score in zip(word_list, projection_scores)}) for word, score in results.items(): print(f"'{word}': {score:.4f}") print(np.round(avg_animals_embeddings[:10], 4))

投影结果为：

'Camel': 0.3887 'Gorilla': 0.4186 'Cheetah': 0.3797 'Dream': 0.2450 'Chair': 0.2823 'Mathematics': 0.1972

在实数轴上绘制上述两组词语的投影：

非常明显的可以看到，上述的avg_vector方向某种程度上代表了一个词语的“动物”属性：即与动物属性相关的词语在该方向的投影大，无关的词语在该方向的投影小。

原理解释

概述

事实上，一组词语Embedding的“平均向量”（centroids of word embeddings），则某种程度的代表这组词语的“语义中心”。如果这组词有某些共性，那么这个平均向量，则可能就是这个共性的代表。

在上述的例子中，刻意地给出的一组词语都是“动物”名称。那么，这个“平均向量”则比较有可能代表了这个向量空间中的“动物”属性。

数学推导

这样考虑这个问题：现在给出的 $ n $ 个向量 $ \alpha_1, \dots , \alpha_n $，找出一个单位向量 $ \xi $ 使得 $ n $ 个向量在 $ \xi $ 向量方向上的投影值的和最大。

这里取 $ \bar{\alpha} = \frac{\sum\limits_{i=1}^{n}\alpha_i}{n} $

目标函数 $ S = \sum\limits_{i=1}^{n}(\alpha_i \cdot \xi ) = \sum\limits_{i=1}^{n}(\alpha_i) \cdot \xi = n \bar{\alpha} \cdot \xi = n \| \bar{\alpha}\| \| \xi \| \cos\theta $

这里 $ n $、$ \bar{\alpha} $都是给定值，而 $ \| \xi \| = 1 $，所以这里 $ \cos\theta $ 取最大值时，上述的目标函数 $ S $ 取最大值。

即：$ \theta = 0 $ 时， $ S $ 取最大值。即当 $ \xi $ 与 $ \bar{\alpha} $ 方向相同时，即 $ \xi = \frac{\bar{\alpha}}{\|\bar{\alpha}\|} $ ，所有向量的投影值的和最大。

投影计算

太久不碰线性代数了，对于基本运算都不是很熟悉了。向量 $ \alpha $ 在 $ \beta $ 方向上的投影长度，计算公式如下：

$$ proj = \frac{\alpha \cdot \beta}{\|\beta\|} $$

证明比较简单，这里不再赘述。

向量的平均方向与主成分方向

当给出一组向量，面对上述问题，比较容易联想到这组向量的“主成分分析”的第一个维度。那么，上述的平均向量和主成分分析的第一个维度有什么关系呢？回答是：没有太大的关系。

可以看下面三个图：

上述三个二维平面中的点的平均方向均为红色，即(1,1)；但是PCA的第一方向则各有不同，有时候与平均向量相同、有时候垂直，有时候相交。总之是没什么关系。

可以看到，平均向量时在当前的“基”下计算获得。而主方向分析的方向，则首先就与原点没有关系。

更深层次的理解

现在的Embedding算法，都是基于现实世界语料库训练而来，反应了人类认知中“语言”与现实世界的对应关系。而在人类的认知中，这个世界是有“维度”的，最为直白的例子就是：我们会将词语划分“褒义词”、“贬义词”。此外，可能还有：动物性、情感强烈度、词性等。那么，在人类认知中这种“认知”有多少个维度呢？这其实是未知的，而各种Embedding算法则是在尝试使用量化的方式描述这些维度。

但是，在实际训练出的各种Embedding实现，例如一个768维的Embedding，其单位向量方向，不太可能是上述的人类“认知”维度。如果把训练出来的Embedding的单位向量记为：$ \alpha_1, \dots , \alpha_n $，而把人类认知的维度记为： $ \beta_1, \dots , \beta_n $ 。

那么，则存在一个过渡矩阵 $T$，可以实现上述向量空间基的变换。

可是，现实世界没有那么理想。Embedding空间确实给出了一组正交基，但是人类认识却很难寻找这样的正交基，例如“动物”属性的词语，可能会带有“情感”属性，例如，“虎狼之词”等，都带有某种情感属性。

虽然，认知很难找到正交的“基”，但是找到某个具体的属性方向，则可以使用本书的方法。这正是本文所描述方法的局限性和价值所在。

补充说明

本文中，所说的Word Embedding，通常是指Sentence Embedding中的Token Embedding。在这里，无需区分两者。

实际的情况更加复杂，例如本文中的“动物”属性，只是这些词所代表的“动物”属性。什么是真正的“动物”属性，并不存在这样的精确概念。人类语言中的“动物”是一个抽象的，并没有数字化、数学化的精确定义。

完整的实现代码，参考：embedding_research_01.py。